Physics

Solved problems in Newton’s laws of motion – Mass, and weight

1. The weight of a 1 kg mass at the surface of the Earth is… g = 9.8 m/s²

Known :

Mass (m) = 1 kg

The acceleration due to gravity at the surface of the Earth (g) = 9.8 m/s²

Wanted: weight (w)

Solution :

w = m g

m = mass (The SI unit of mass is the kilogram, kg)

g = acceleration due to gravity (The SI unit of g is m/s²)

w = weight (The SI unit of w is kg m/s² or Newton)

Weight :

w = (1 kg)(9.8 m/s²) = 9.8 kg m/s² = 9.8 Newton

2.

(a) Draw the force of gravity (weight) that act on the object when the object is at rest on a table, as shown in figure (a).

(b) Draw the force of gravity (weight) and it’s components that act on an object sliding down an inclined plane, as shown in figure (b)

Solution

The direction of the weight is downward toward the center of the Earth.

w_x = the horizontal component of the weight and w_y = the vertical component of the weight

3. The mass of a box is 1 kg and acceleration due to gravity is 9.8 m/s². Find (a) weight (b) the horizontal component and the vertical component of the weight.

Solution

Weight : w = m g = (1 kg)(9.8 m/s²) = 9.8 kg m/s² = 9.8 Newton

The horizontal component of the weight :

w_x = w sin 30^o = (9,8 N)(0,5) = 4.9 Newton

The vertical component of the weight :

w_y = w cos 30^o = (9.8 N)(0.5√3) = 4.9√3 Newton

[wpdm_package id=’458′]

1. Mass and weight
2. Normal force
3. Newton’s second law of motion
4. Friction force
5. Motion on the horizontal surface without friction force
6. The motion of two bodies with the same acceleration on the rough horizontal surface with the friction force
7. Motion on the inclined plane without friction force
8. Motion on the rough inclined plane with the friction force
9. Motion in an elevator
10. The motion of bodies connected by cord and pulley
11. Two bodies with the same magnitude of accelerations
12. Rounding a flat curve – dynamics of circular motion
13. Rounding a banked curve – dynamics of circular motion
14. Uniform motion in a horizontal circle
15. Centripetal force in uniform circular motion

Read more

Solved Problems in Linear Motion – Up and down motion in free fall

1. A person throws a ball upward into the air with an initial velocity of 20 m/s. Calculate how high it goes. Ignore air resistance. Acceleration due to gravity (g) = 10 m/s².

Solution

We use one of these kinematic equations for motion at constant acceleration, as shown below.

v_t = v_o + a t

s = v_o t + ½ a t²

v_t² = v_o² + 2 a s

Known :

We choose the upward direction as positive and downward direction as negative.

Initial velocity (v_o) = 20 m/s (positive upward)

Acceleration of gravity (g) = – 10 m/s² (negative downward).

Final velocity (v_t) = 0 (it’s speed is zero for an instant at highest point)

Wanted : Maximum height (h)

Solution :

v_t² = v_o² + 2 g h

0 = (20²) + 2(-10) h

0 = 400 – 20 h

400 = 20 h

h = 400 / 20 = 40 / 2 = 20 meters

2. A person throws a stone upward at 20 m/s while standing on the edge of a cliff, so that the stone can fall to the base of the cliff 100 meters below.

(a) How long does it take the ball to reach the base of the cliff (b) Final velocity just before stone strikes the ground. Acceleration due to gravity (g) = 10 m/s². Ignore air resistance.

Known :

We choose the upward direction as positive and downward direction as negative.

High (h) = -100 meters (negative because final position below initial position)

Initial velocity (v_o) = 20 m/s (positive upward)

Acceleration of gravity (g) = -10 m/s² (negative downward)

Wanted :

(a) Time in air or time interval (t)

(b) Final velocity (v_t)

Solution :

(a) Time interval (t)

Known :

High (h) = -100 meters (negative because final position below initial position)

Initial velocity (v_o) = 20 m/s (positive upward), Acceleration of gravity (g) = -10 m/s² (negative downward).

h = v_o t + ½ g t²

-100 = (20) t + ½ (-10) t²

-100 = 20 t – 5 t²

-5 t² + 20 t + 100 = 0

We use quadratic formula :

(b) Final velocity

v_t² = v_o² + 2 g h

v_t² = (20²) + 2 (-10)(-100)

v_t² = 400 + 2000

v_t² = 2400

v_t = 49 m/s

[wpdm_package id=’515′]

[wpdm_package id=’517′]

1. Distance and displacement
2. Average speed and average velocity
3. Constant velocity
4. Constant acceleration
5. Free fall motion
6. Down motion in free fall
7. Up and down motion in free fall

Read more

Solved Problems in Linear Motion – Down motion in free fall

1. A ball is thrown vertically downward with initial speed 10 m/s and reach the ground in 2 seconds. Find final speed just before the ball hits the ground. Acceleration of gravity (g) = 10 m/s². Ignore air resistance.

Known :

Initial velocity (v_o) = 10 m/s

Time elapsed (t) = 2 seconds

Acceleration of gravity (g) = 10 m/s²

Wanted : Final velocity (v_t)

Solution :

Acceleration 10 m/s² means speed increase by 10 m/s each second. After 3 second, speed = 30 m/s.

Final velocity = 10 m/s + 20 m/s = 30 m/s.

Kinematic equations for motion at constant acceleration, as shown below :

v_t = v_o + a t ………. 1

h = v_o t + ½ a t² ………. 2

v_t² = v_o² + 2 a h ………. 3

v_t = v_o + g t

v_t = 10 + (10)(2)

v_t = 10 + 20 = 30 m/s

Final velocity = v_t = 30 m/s

2. A stone is thrown vertically downward from a bridge with initial speed 5 m/s and reach the water in 2 seconds. Calculate the height of the bridge.

Known :

Initial velocity (v_o) = 5 m/s

Time elapsed (t) = 2 seconds

Acceleration due to gravity (g) = 10 m/s²

Wanted : the height of the bridge (h)

Solution :

h = v_o t + ½ g t²

h = (5)(2) + ½ (10)(2)²

h = 10 + (5)(4)

h = 10 + 20

h = 30 meters

3. A ball is thrown vertically downward with initial speed 10 m/s from a height of 80 meters. Find (a) Time in air (b) Final velocity just before ball strikes the ground.

Known :

height (h) = 80 meters

Initial velocity (v_o) = 10 m/s

Acceleration of gravity (g) = 10 m/s²

Wanted :

(a) Time interval (t)

(b) Final velocity (v_t)

Solution :

(a) Time interval (t)

Final velocity :

v_t² = v_o² + 2 g h

v_t² = (10)² + 2(10)(80) = 100 + 1600 = 1700

v_t = 41 m/s

Time interval (t) :

v_t = v_o + g t

41 = 10 + (10)(t)

41 – 10 = 10 t

31 = 10 t

t = 31 / 10 = 3,1 seconds

(b) Final velocity (v_t) ?

v_t = 41 m/s

[wpdm_package id=’513′]

[wpdm_package id=’517′]

1. Distance and displacement
2. Average speed and average velocity
3. Constant velocity
4. Constant acceleration
5. Free fall motion
6. Down motion in free fall
7. Up and down motion in free fall

Read more

Solved Problems in Linear Motion – Freely falling objects

1. An object dropped from the top of a cliff. It is seen to hit the ground below after 3 seconds. Determine its velocity just before hitting the ground. Acceleration of gravity is 10 m/s². Ignore air resistance.

Known :

Initial velocity (v_o) = 0 (object dropped)

Time interval (t) = 3 seconds

Acceleration of gravity (g) = 10 m/s²

Wanted : Final velocity (v_t)

Solution :

Acceleration due to gravity at the surface of the earth, its magnitude is 9.8 m/s². To make calculation easier, we use 10 m/s².

10 m/s² or 10 m/s / 1 second, means that the speed increases linearly in time by 10 m/s during each second.

After 1 second, object’s speed = 10 m/s

After 2 seconds, object’s speed = 20 m/s

After 3 seconds, object’s speed = 30 m/s.

We also can use kinematic equations for motion at a constant acceleration, as shown below.

v_t = v_o + a t

s = v_o t + ½ a t²

v_t² = v_o² + 2 a s

Free fall has no initial velocity (v_o = 0), so above equation can be changed as shown below :

Equation of Free fall motion :

v_t = g t ………… 1

h = ½ g t² ………… 2

v_t² = 2 g h ………….. 3

v_t = g t

v_t = (10)(3)

v_t = 30 m/s

Final velocity is 30 m/s

2. A body falls freely from rest, from a height of 25 m. Find (a) The speed with which it strikes the ground. (b) The time it takes to reach the ground.

Acceleration due to gravity at the surface of Earth is 10 m/s².

Known :

Height (h) = 5 meters

Acceleration of gravity (g) = 10 m/s²

Wanted :

(a) Final velocity (v_t)

(b) Time interval (t)

Solution :

Free fall’s equation :

v_t = g t

h = ½ g t²

v_t² = 2 g h

(a) Final velocity (v_t)

v_t² = 2 g h = 2(10)(5) = 100

v_t = 10 m/s

(b) Time interval (t)

h = ½ g t²

5 = ½ (10) t²

5 = 5 t²

t² = 5/5 = 1

t = 1 second

3. A ball dropped from a height. Find (a) Acceleration (b) Distance after 3 seconds (c) Time in air if final velocity is 20 m/s. Acceleration due to gravity = 10 m/s²

Known :

Acceleration of gravity (g) = 10 m/s²

Wanted :

(a) Acceleration (a)

(b) Distance or height (h) if time elapsed (t) = 3 seconds

(c) Time interval (t) if v_t = 20 m/s

Solution :

Free fall’s equation :

v_t = g t

h = ½ g t²

v_t² = 2 g h

(a) Acceleration (a)

Acceleration = acceleration due to gravity = 10 m/s². It means speed increase by 10 m/s each second.

(b) Distance or height (h) after t = 3 seconds

h = ½ g t² = ½ (10)(3)² = (5)(9) = 45 meters

(c) Time elapsed (t) if v_t = 20 m/s

v_t = g t

20 = (10) t

t = 20 / 10 = 2 seconds

[wpdm_package id=’511′]

[wpdm_package id=’517′]

1. Distance and displacement
2. Average speed and average velocity
3. Constant velocity
4. Constant acceleration
5. Free fall motion
6. Down motion in free fall
7. Up and down motion in free fall

Read more

Solved Problems in Linear Motion – Constant acceleration

1. A car accelerates from rest to 20 m/s in 10 seconds. Determine the car’s acceleration!

Solution

Known :

Initial velocity (v_o) = 0 (rest)

Time interval (t) = 10 seconds

Final velocity (v_t) = 20 m/s

Wanted : Acceleration (a)

Solution :

v_t = v_o + a t

20 = 0 + (a)(10)

20 = 10 a

a = 20 / 10

a = 2 m/s²

2. A car is decelerating from 30 m/s to rest in 10 seconds. Determine car’s acceleration.

Solution

Known :

Initial velocity (v_o) = 30 m/s

Final velocity (v_t) = 0

Time interval (t) = 10 seconds

Wanted : acceleration (a)

Solution :

v_t = v_o + a t

0 = 30 + (a)(10)

– 30 = 10 a

a = – 30 / 10

a = -3 m/s²

The negative sign appears because the final velocity is less than the initial velocity.

3. A car starts and accelerates at a constant 4 m/s² in 1 second. Determine speed and distance after 10 seconds.

Solution

(a) Speed

Acceleration 4 m/s² means speed increase 4 m/s every 1 second. After 2 seconds, car’s speed is 8 m/s. After 10 seconds, car’s speed is 40 m/s.

(b) Distance

Known :

Initial velocity (v_o) = 0

Final velocity (v_t) = 40 m/s

Acceleration (a) = 4 m/s²

Wanted : Distance

Solution :

s = v_o t + ½ a t² = 0 + ½ (4)(10²) = (2)(100) = 200 meters

4. A car travels at a constant 10 m/s, then decelerates at a constant 2 m/s² until rest. Determine time elapsed and car’s distance before rest.

Known :

Initial velocity (v_o) = 10 m/s

Acceleration (a) = -2 m/s² (The negative sign appears because the final velocity is less than the initial velocity)

Final velocity (v_t) = 0 (rest)

Wanted : Time interval and distance

Solution :

(a) Time interval (t)

v_t = v_o + a t

0 = 10 + (-2)(t)

0 = 10 – 2 t

10 = 2 t

t = 10 / 2 = 5 seconds

(b) Distance

v_t² = v_o² + 2 a s

0 = 10² + 2(-2) s

0 = 100 – 4 s

100 = 4 s

s = 100 / 4 = 25 meters

5. A car travels at 40 m/s, decelerates at a constant 4 m/s² until rest. Determine speed and distance after decelerating in 10 seconds!

Solution

Known :

Initial velocity (v_o) = 40 m/s

Acceleration (a) = -4 m/s²

Time interval (t) = 10 seconds

Wanted : final velocity (v_t) and distance (s)

Solution :

(a) Final velocity

v_t = v_o + a t = 40 + (-4)(10) = 40 – 40 = 0 m/s

0 m/s means car rest.

(b) Distance

s = v_o t + ½ a t² = (40)(10) + ½ (-4)(10²) = 400 + (-2)(100) = 400 – 200 = 200 meters

6. Determine distance after 10 seconds!

Solution

Distance : s = v t = (10-0)(5-0) = (10)(5) = 50 meters

7. Determine distance after 4 seconds!

Solution

Distance = square area + triangular area

Distance = (8-0)(8-0) + ½ (16-8)(8-0) = (8)(8) + ½ (8)(8) = 64 + 32 = 96 meters

8. Determine car’s distance after 4 seconds!

Solution

Distance = triangular area = ½ (4-0)(8-0) = ½ (4)(8) = 16 meters

9. A car moves at 90 km/h past a police car that stops by the side of the road. One minute later, the police car chases at 0.8 m/s². How far the police car reaches the car?

Known :

The speed of car (v) = 90 km/hour = 90,000 meters / 3600 seconds = 25 meters/second

Time interval (t) = 1 minute = 60 seconds

Acceleration of police’s car (a) = 0.8 m/s²

Initial velocity of police’s car (v_o) = 0 m/s

Wanted : Distance traveled by police’s car

Solution :

The car moves at a constant velocity. Distance traveled by the car :

Initial distance :

s = v t = (25)(60) = 1500 meters

Final distance :

s = v t = (25)(t)

Total distance = 1500 + 25 t

Police’s car moving at a constant acceleration. Distance traveled by police’s car :

s = v_o t + ½ a t² = (0)(t) + ½ (0.8)(t²) = 0 + 0.4 t² = 0.4 t²

When the police’s car reaches the the car, distance traveled by police’s car same as distance traveled by the car.

Distance traveled by car = distance traveled by police’s car

1500 + 25 t = 0.4 t²

0.4 t² – 25 t – 1500 = 0

Use quadratic formula :

Distance traveled by police’s car :

s = 0.4 t² = (0.4)(100²) = (0.4)(10,000) = 4000 meters = 4 km

10. A car moves at a constant 24 m/s brakes so that it has a constant deceleration of 0.952 m/s². Determine the speed of the car after a distance of 250 meters.

Known :

Initial velocity (v_o) = 24 m/s

Acceleration (a) = – 0.952 m/s² (negative signed because deceleration)

Distance (d) = 250 meters

Wanted : Car’s speed after 250 meters

Solution :

Known : initial speed (v_o), acceleration (a), distance (d), wanted : final speed (v_t) so use the equation of v_t² = v_o² + 2 a d

v_t = final velocity, v_o = initial velocity, a = acceleration, d = distance

v_t² = (24)² + (2)(-0.952)(250)

v_t² = 576 – 476

v_t² = 100

v_t = √100

v_t = 10 m/s

[wpdm_package id=’507′]

[wpdm_package id=’517′]

1. Distance and displacement
2. Average speed and average velocity
3. Constant velocity
4. Constant acceleration
5. Free fall motion
6. Down motion in free fall
7. Up and down motion in free fall

Read more

Solved Problems in Linear Motion – Constant velocity

1. A car travels at a constant 10 m/s. Determine distance after 10 seconds and 60 seconds.

Solution

Constant speed 10 meters/second means car travels 10 meters every 1 second.

After 2 seconds, the car travels 20 meters,

After 5 seconds, the car travels 50 meters,

After 10 seconds, the car travels 100 meters,

After 60 seconds, the car travels 600 meters.

2. A car travels along a straight road at constant 72 km/h. Determine the car’s distance after 2 minutes and 5 minutes.

Solution

72 km/h = (72)(1000 meters) / 3600 seconds = 72,000 / 3600 seconds = 20 meters/second.

The constant speed at 20 meters/second means car travels 20 meters every 1 second.

After 120 seconds or 2 minutes, car travels 20 meters x 120 = 2400 meters,

After 300 seconds or 5 minutes, car travels 20 meters x 300 = 6000 meters.

3. A body travels along a straight road for 100 meters in 50 seconds. Determine the speed of the body.

Solution

100 meters / 50 seconds = 10 meters / 5 seconds = 2 meters/second.

4. Determine speed according to the diagram below….

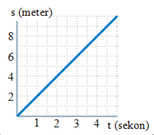Solution

Speed = Distance / time elapsed

Speed = 2 meters / 1 second = 4 meters / 2 seconds = 6 meters / 3 seconds = 8 meters / 4 seconds = 2 meters/second.

5. Cars A and B approach each other on parallel tracks. When the distance between the two cars is 100 meters, car A moves at a constant speed of 10 m/s, car B moves at a constant speed of 40 m/s. Determine (a) the distance of car A before passing car B (b) time interval before car B passing car A.

Solution

Car A moving with a constant speed at 10 meters/second, means car A moves as far as 10 meters every 1 second. After 2 seconds, A car move as far as 20 meters.

Car B moves with a constant speed at 40 meters/second, means car B moves as far as 40 meters every 1 second. After 2 seconds, car B moves as far as 80 meters.

20 meters + 80 meters = 100 meters.

(a) The distance of car A before passing car B is 20 meters. The distance of car B before passing car A is 80 meters.

(b) Time interval of car B before passing car A is 2 seconds. Time interval of car A before passing car B is 2 seconds

5. If the speedometer of a car shows 108 km/h, determine the distance traveled by car in one minute.

Solution :

The speedometer is an instrument to measure speed. The speed of a car is 108 km/hour.
108 km / h = (108) (1000 meters) / 3600 seconds = 30 meters/second.

1 minute = 60 seconds

The speed of the car 30 meters/second means the car moves as far as 30 meters in 1 second.

After 1 second, the car moves as far as 1 x 30 meters = 30 meters.

After 2 seconds, the car moves as far as 2 x 30 meters = 60 meters.

After 60 seconds, the car moves as far as 60 x 30 meters = 1800 meters.

6. Tom throws a ball straight to Andrew. Tom and Andrew are separated as far as 10.08 meters. The ball is thrown horizontally and moves at 20 m/s (ignore gravity). Andrew hits the ball 4.00 x 10^-3 seconds after the ball was thrown. If the hitter moves at a constant speed of 5.00 m/s, the ball is hit by the hitter after the hitter moves as far as…

Known :

The distance between Tom and Andrew = 10.08 meters

Ball’s speed (v) = 20 m/s

The time interval (t) = 4 x 10^-3 seconds = 0.004 seconds

Hitter’s speed (v) = 5 m / s

Wanted: The ball is hit by hitter after the ball moves as far as…

Solution :

Ball’s distance :

s₁ = v t = (20) (0.004) = 0.08 meters

Hitter’s distance :

s₂ = v t = 5 t

Ball’s distance + hitter’s distance = distance between Tom and Andrew.

0.08 + 5 t = 10.08

5 t = 10.08 – 0.08

5 t = 10

t = 10/5

t = 2 seconds

Hitter’s distance :

s₂ = v t = 5 t = (5) (2) = 10 meters

7. A hunter with his car is chasing a deer. The car moves at 72 km/h and the deer run at speeds of 64.8 km/h. When the distance between the car and the deer is 2012 meters, the hunter fired his shotgun. Bullets out of the gun at 200 m/s. Determine the time interval of the deer getting shot.

A. 0.5 s

B. 1 s

C. 1.25 s

D. 1.5 s

Known :

Speed of car (v_b) = 72 km/h = (72)(1000 m) / 3600 s = 20 m/s

Speed of deer (v_r) = 64.8 km/h = (64.8)(1000 m) / 3600 s = 64800 m / 3600 s = 18 m/s

When the bullet is fired, the distance between the car and the deer (s) = 202 meters

Speed of fire (v_p) = 20 m/s + 200 m/s = 220 m/s

Weapons held by hunters who are in a car that moves with a speed of 20 m/s so that the speed of car is also added to the speed of the bullet.

Wanted: Determine the time interval of the deer getting shot

Solution :

Think of cars and deer moving at a constant velocity.

Equation : v = s / t or s = v t

v = speed, s = distance, t = time interval

Distance = 202 + X_r = 202 + v_r t = 202 + 18 t

Distance = Y_p = v_p t = 220 t

Distance traveled by deer = distance traveled by bullet

202 + 18 t = 220 t

202 = 220 t – 18 t

202 = 202 t

t = 202/202

t = 1 second

The correct answer is B.

[wpdm_package id=’507′]

[wpdm_package id=’517′]

1. Distance and displacement
2. Average speed and average velocity
3. Constant velocity
4. Constant acceleration
5. Free fall motion
6. Down motion in free fall
7. Up and down motion in free fall

Read more

Solved Problems in Linear Motion – Average speed and average velocity

1. A car travels along a straight road to the east for 100 meters in 4 seconds, then go the west for 50 meters in 1 second. Determine average speed and average velocity.

Solution

Distance = 100 meters + 50 meters = 150 meters

Displacement = 100 meters – 50 meters = 50 meters, to east.

Time elapsed = 4 seconds + 1 second = 5 seconds.

Average speed = Distance / time elapsed = 150 meters / 5 seconds = 30 meters/second.

Average velocity = Displacement / time elapsed = 50 meters / 5 seconds = 10 meters/second.

2. A person walks 4 meters east in 1 second, then walks 3 meters north in 1 second. Determine average speed and average velocity.

Solution

Distance = 4 meters + 3 meters = 7 meters

Displacement = = meters, to northeast.

Time elapsed = 1 second + 1 second = 2 seconds.

Average speed = distance / time elapsed = 7 meters / 2 seconds = 3.5 meters/second

Average velocity = displacement / time elapsed = 5 meters / 2 seconds = 2.5 meters/second

3. A runner travels around rectangle track with length = 50 meters and width = 20 meters. After travels around rectangle track two times, runner back to starting point. If time elapsed = 100 seconds, determine average speed and average velocity.

Solution

Circumference of rectangle = 2(50 meters) + 2(20 meters) = 100 meters + 40 meters = 140 meters.

Travels around rectangle 2 times = 2(140 meters) = 280 meters.

Distance = 280 meter.

Displacement = 0 meter. (runner back to start point)

Average speed = distance / time elapsed = 280 meters / 100 seconds = 2.8 meters/second.

Average velocity = displacement / time elapsed = 0 / 100 seconds = 0.

[wpdm_package id=’505′]

[wpdm_package id=’517′]

1. Distance and displacement
2. Average speed and average velocity
3. Constant velocity
4. Constant acceleration
5. Free fall motion
6. Down motion in free fall
7. Up and down motion in free fall

Read more

Solved problems in vectors – determine resultant of two vectors using components of the vector

1. F₁ = 6 N, F₂ = 10 N. Determine resultant vector.

Solution

F_1x = F₁ cos 60^o = (6)(0.5) = 3 N (positive because it has same direction with x axis)

F_2x = F₂ cos 30^o = (10)(0.5√3) = 5√3 = (5)(1.372) = -8.66 N (negative because it has same direction with -x axis)

F_1y = F₁ sin 60^o = (6)(0.5√3) = 3√3 = (3)(1.372) = 4.116 N (positive because it has same direction with y axis)

F_2y = F₂ sin 30^o = (10)(0.5) = -5 N (negative because it has same direction with -y axis)

F_x = F_1x – F_2x = 3 – 8.66 = -5.66 N

F_y = F_1y – F_2y = 4.116 – 5 = -0.884 N

Resultant of these two forces is 5.7 N.

2. F₁ = 4 N, F₂ = 4 N, F₃ = 8 N. Determine resultant vector.

Solution

F_1x = F₁ cos 60^o = (4)(0.5) = 2 N (positive because it has same direction with x axis)

F_2x = -4 N (negative because it has same direction with -x axis)

F_3x = F₃ cos 60^o = (8)(0.5) = 4 N (positive because it has same direction with x axis)

F_1y = F₁ sin 60^o = (4)(0.5√3) = 2√3 N (positive because it has same direction with y axis)

F_2y = 0

F_3y = F₃ sin 60^o = (8)(0.5√3) = -4√3 N (negative because it has same direction with -y axis)

F_x = F_1x – F_2x + F_3x = 2 – 4 + 4 = 2 N

F_y = F_1y + F_2y – F_3y = 2√3 + 0 – 4√3 = -2√3 N

Resultant of these three forces is 5.7 N.

[wpdm_package id=’542′]

[wpdm_package id=’554′]

1. Determine the resultant of in a line vector
2. Determine vector components
3. Determine the resultant of two vectors using the Pythagorean theorem
4. Determine the resultant of two vectors using cosines equation
5. Determine the resultant of two vectors using components of vectors

Read more

Solved problems in vectors – determine resultant of two vectors using cosines equation

1. F₁ = 10 N and F₂ = 20 N. Determine resultant vector.

2. A₁ = 15 and A₂ = 9. The angle between the two vectors is 60^o. Determine the resultant vector.

Solution

3. v₁ = 5 and v₂ = 12. The angle between the two vectors is 90^o. Determine the resultant vector.

Solution

[wpdm_package id=’542′]

[wpdm_package id=’554′]

1. Determine the resultant of in a line vector
2. Determine vector components
3. Determine the resultant of two vectors using the Pythagorean theorem
4. Determine the resultant of two vectors using cosines equation
5. Determine the resultant of two vectors using components of vectors

Read more