Hooke’s law – problems and solutions

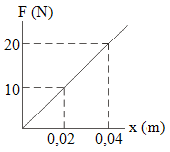
1. A graph of force (F) versus elongation (x) shown in the figure below. Find the spring constant!

Solution

Hooke’s law formula :

k = F / x

F = force (Newton)

k = spring constant (Newton/meter)

x = the change in length (meter)

Spring constant :

k = 10 / 0.02 = 20 / 0.04

k = 500 N/m

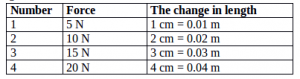
2. Determine the spring constant.

Solution

Spring constant :

k = F / x

k = 5 / 0.01 = 10 / 0.02 = 15 / 0.03 = 20 / 0.04

k = 500 N/m

3. Spring A has the original length of 60 cm and spring B has the original length of 90 cm. Spring A has constant 100 N/m, spring B has constant 200 N/m. The ratio of the change in length of spring A to the change in length of spring B is…

Known :

Constant of spring A (k_A) = 100 N/m

Constant of spring B (k_B) = 200 N/m

Force on spring A (F_A) = F

Force on spring B (F_B) = F

Wanted: Δl_A : Δl_B

Solution :

Hooke’s law formula :

Δl = F / k

Δl = the change in length, F = force, k = constant

The change in length of spring A :

Δl_A = F_A / k_A = F / 100

The change in length of spring B :

Δl_B = F_B / k_B = F / 200

The ratio of the change in length of spring A to the change in length of spring B :

Δl_A : Δl_B

F / 100 : F / 200

1 / 100 : 1 / 200

1 / 1 : 1 / 2

2 : 1

4. A nylon string with original length 20 cm, is pulled by a force of 10 N. The change in length of the string is 2 cm. Determine the magnitude of force if the change in length is 6 cm.

Known :

Force (F) = 10 N

The change in length (Δl) = 2 cm = 0.02 m

Wanted : the magnitude of force (F) if Δl = 0.06 m.

Solution :

Constant :

k = F / Δl

k = 10 / 0.02 = 500 N/m

The magnitude of force (F) if Δl = 0.06 m :

F = k x

F = (500)(0.06)

F = 30 N

[wpdm_package id=’689′]

1. Hooke’s law
2. Stress, strain, Young’s modulus