Motion on the rough inclined plane with the friction force – application of Newton’s law of motion problems and solutions

1. Object’s mass = 2 kg, acceleration due to gravity = 9.8 m/s², coefficient of the static friction = 0.2, coefficient of the kinetic friction = 0.1. Is the object at rest or accelerating? If the object is accelerated, find (a) the net force (b) magnitude and direction of the box’s acceleration!

Solution

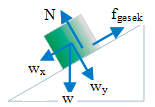
Known :

Mass (m) = 2 kg

Acceleration due to gravity (g) = 9.8 m/s²

Coefficient of the static friction (μ_s) = 0.2

Coefficient of the kinetic friction (μ_k) = 0.1

Weight (w) = m g = (2)(9.8) = 19.6 Newton

The horizontal component of the weight (w_x) = w sin 30^o = (19.6)(0.5) = 9.8 Newton

The vertical component of th weight (w_y) = w cos 30^o = (19.6)(0.5√3) = 9.8√3 Newton

The normal force (N) = w_y = 9.8√3 Newton

Force of the static friction (f_s) = (0.2)(9.8√3) = 1.96√3 Newton = 3.39 Newton

Force of the kinetic friction (f_k) = (0.1)(9.8√3) = 0.98√3 Newton = 1.69 Newton

Solution :

Object is at rest if w_x < f_s, object is moving down if w_x > f_s.

w_x = 9.8 Newton and f_s = 3.39 Newton.

(a) the net force

∑F = w_x – f_k = 9.8 – 1.69 = 8.11 Newton

(b) magnitude and direction of the acceleration

∑F = m a

8.11 = (2) a

a = 4.05

Magnitude of the acceleration = 4.05 m/s² and direction of the acceleration = downward.

2. Object’s mass = 4 kg, acceleration due to gravity = 9,8 m/s². Coefficient of the kinetic friction = 0.2 and coefficient of the static friction = 0.4. Magnitude of the force F = 40 Newton. The object is at rest or slides down ? If the object slides down, find (a) the net force (b) magnitude and direction of the acceleration!

Solution

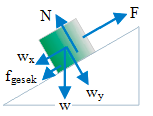
Known :

Mass (m) = 4 kg

Acceleration due to gravity (g) = 9.8 m/s²

The coefficient of the static friction (μ_s) = 0.4

The coefficient of the kinetic friction (μ_k) = 0.2

Weight (w) = m g = (4)(9.8) = 39.2 Newton

The horizontal component of the weight (w_x) = w sin 30^o = (39.2)(0.5) = 19.6 Newton

The vertical component of the weight (w_y) = w cos 30^o = (392)(0..5√3) = 19.6√3 Newton

The normal force (N) = w_y = 19.6√3 Newton = 33.95 Newton

the static friction force (f_s) = μ_s N = (0,4)(33.95) = 13.58 Newton

The kinetic friction force (f_k) = μ_k N = (0.2)(33.95) = 6.79 Newton

F = 40 Newton

Solution :

The object slides down if F < w_x + f_s. The object slides up if F > w_x + f_s.

F = 40 Newton, w_x = 19.6 Newton and f_s = 13.58 Newton.

F is greater than w_x + f_s so the object slides up.

(a) The net force

∑F = F – w_x – f_k = 40 – 19.6 – 6.79 = 13.61 Newton

(b) The magnitude and direction of the acceleration

∑F = m a

6.4 = (4) a

a = 1.6

The magnitude of the acceleration is 1.6 m/s² and direction of the acceleration is upward.

[wpdm_package id=’481′]

1. Mass and weight
2. Normal force
3. Newton’s second law of motion
4. Friction force
5. Motion on the horizontal surface without friction force
6. The motion of two bodies with the same acceleration on the rough horizontal surface with the friction force
7. Motion on the inclined plane without friction force
8. Motion on the rough inclined plane with the friction force
9. Motion in an elevator
10. The motion of bodies connected by cord and pulley
11. Two bodies with the same magnitude of accelerations
12. Rounding a flat curve – dynamics of circular motion
13. Rounding a banked curve – dynamics of circular motion
14. Uniform motion in a horizontal circle
15. Centripetal force in uniform circular motion