Newton’s second law of motion – problems and solutions

Solved problems in Newton’s laws of motion – Newton’s second law of motion 

1. A 1 kg object accelerated at a constant 5 m/s². Estimate the net force needed to accelerate the object.

Known :

Mass (m) = 1 kg

Acceleration (a) = 5 m/s²

Wanted : net force (∑F)

Solution :

We use Newton’s second law to get the net force.

∑F = m a

∑F = (1 kg)(5 m/s²) = 5 kg m/s² = 5 Newton

2. Mass of an object = 1 kg, net force ∑F = 2 Newton. Determine the magnitude and direction of the object’s acceleration….

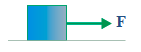
Known :

Mass (m) = 1 kg

Net force (∑F) = 2 Newton

Wanted : The magnitude and direction of the acceleration (a)

Solution :

a = ∑F / m

a = 2 / 1

a = 2 m/s²

The direction of the acceleration = the direction of the net force (∑F)

3. Object’s mass = 2 kg, F₁ = 5 Newton, F₂ = 3 Newton. The magnitude and direction of the acceleration is…

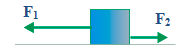
Known :

Mass (m) = 2 kg

F₁ = 5 Newton

F₂ = 3 Newton

Wanted : The magnitude and direction of the acceleration (a)

Solution :

net force :

∑F = F₁ – F₂ = 5 – 3 = 2 Newton

The magnitude of the acceleration :

a = ∑F / m

a = 2 / 2

a = 1 m/s²

Direction of the acceleration = direction of the net force = direction of F₁

4. Object’s mass = 2 kg, F₁ = 10 Newton, F₂ = 1 Newton. The magnitude and direction of the acceleration is…

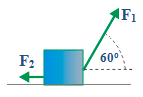
Known :

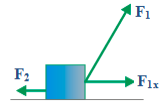
Mass (m) = 2 kg

F₂ = 1 Newton

F₁ = 10 Newton

F_1x = F₁ cos 60^o = (10)(0.5) = 5 Newton

Wanted : The magnitude and direction of the acceleration (a)

Solution :

Net force :

∑F = F_1x – F₂ = 5 – 1 = 4 Newton

The magnitude of the acceleration :

a = ∑F / m

a = 4 / 2

a = 2 m/s²

Direction of the acceleration = direction of the net force = direction of F_1x

5. F₁ = 10 Newton, F₂ = 1 Newton, m₁ = 1 kg, m₂ = 2 kg. The magnitude and direction of the acceleration is…

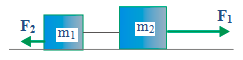
Known :

Mass 1 (m₁) = 1 kg

Mass 2 (m₂) = 2 kg

F₁ = 10 Newton

F₂ = 1 Newton

Wanted : The magnitude and direction of the acceleration (a)

Solution :

The net force :

∑F = F₁ – F₂ = 10 – 1 = 9 Newton

The magnitude of the acceleration :

a = ∑F / (m₁ + m₂)

a = 9 / (1 + 2)

a = 9 / 3

a = 3 m/s²

The direction of the acceleration = the direction of the net force = direction of F₁

6.

A 40-kg block accelerated by a force of 200 N. Acceleration of the block is 3 m/s². Determine the magnitude of friction force experienced by the block.

A. 15 N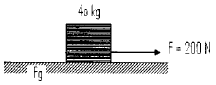

B. 40 N

C. 43 N

D. 80 N

Known :

Mass (m) = 40 kg

Force (F) = 200 N

Acceleration (a) = 3 m/s²

Wanted: Friction force (F_g)

Solution :

The equation of Newton’s second law of motion

∑F = m a

∑F = net force, m = mass, a = acceleration

The direction of force F rightward, the direction of friction force leftward (the direction of friction force is opposite with the direction of object’s motion).

Choose rightward as positive and leftward as negative.

∑F = m a

F – F_g = m a

200 – F_g = (40)(3)

200 – F_g = 120

F_g = 200 – 120

F_g = 80 Newton

The correct answer is D.

7. Block A with a mass of 100-gram place above block B with a mass of 300 gram, and then block b pushed with a force of 5 N vertically upward. Determine the normal force exerted by block B on block A.

A. 1 N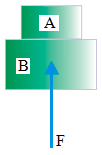

B. 1.25 N

C. 2 N

D. 3 N

Known :

Force (F) = 5 Newton

Mass of block A (m_A) = 100 gram = 0.1 kg

Mass of block B (m_B) = 300 gram = 0.3 kg

Acceleration of gravity (g) = 10 m/s²

Weight of block A (w_A) = (0.1 kg)(10 m/s²) = 1 kg m/s² = 1 Newton

Weight of block B (w_B) = (0.3 kg)(10 m/s²) = 3 kg m/s² = 3 Newton

Wanted : Normal force exerted by block B to block A

Solution :

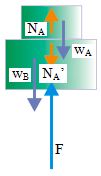There are several forces that act on both block, as shown in figure.

F = push force (act on block B)

w_A = weight of block A (act on block A)

w_B = weight of block B (act on block B)

N_A = normal force exerted by block B on block A (Act on block A)

N_A’ = normal force exerted by block A on block B (Act on block B)

Apply Newton’s second law of motion on both blocks :

∑F = m a

F – w_A – w_B + N_A – N_A’ = (m_A + m_B) a

N_A and N_A’ are action-reaction forces that have the same magnitude but opposite in direction so eliminated from the equation.

F – w_A – w_B = (m_A + m_B) a

5 – 1 – 3 = (0.1 + 0.3) a

5 – 4 = (0.4) a

1 = (0.4) a

a = 1 / 0.4

a = 2.5 m/s²

Apply Newton’s second law of motion on block A :

∑F = m a

N_A – w_A = m_A a

N_A – 1 = (0.1)(2.5)

N_A – 1 = 0.25

N_A = 1 + 0.25

N_A = 1.25 Newton

The correct answer is B.

8. An object with weight of 4 N supported by a cord and pulley. A force of 2 N acts on the block and one end of the cord pulled by a force of 9 N. Determine the net force acts on object X.

A. 3 N upward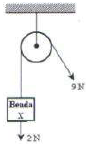

B. 4 N downward

C. 9 N upward

D. 9 N downward

Known :

Weight of X (w_X) = 4 Newton

Pull force (F_x) = 2 Newton

Tension force (F_T) = 9 Newton

Wanted: Net force acts on object X

Solution :

Vertically upward forces that act on object X :

The tension force has the same magnitude in all part of the cord. So the tension force is 9 N.

Vertically downward forces that act on object X :

There are two forces that act on object X and both forces are vertically downward, the horizontal component of weight w_x and the horizontal component of force F_x.

Net force act on the object X :

F_T – w_X – F_x = 9 – 4 – 2 = 9 – 6 = 3

The net force act on the object X is 3 Newton, vertically upward.

The correct answer is A.

9. An object initially at rest on a smooth horizontal surface. A force of 16 N acts on the object so the object accelerated at 2 m/s². If the same object at rest on a rough horizontal surface so the friction force acts on the object is 2 N, then determine the acceleration of the object if the same force of 16 N acts on the object.

A. 1.75 m/s²

B. 1.50 m/s²

C. 1.00 m/s²

D. 0.88 m/s²

Known :

Force (F) = 16 Newton = 16 kg m/s²

Acceleration (a) = 2 m/s²

Friction force (F_fric) = 2 Newton = 2 kg m/s²

Wanted : Object’s acceleration ?

Solution :

Smooth horizontal surface (no friction force) :

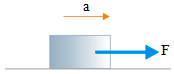∑F = m a

F = m a

16 = (m) 2

m = 16 / 2

m = 8 kg

Mass of object is 8 kilogram.

Rough horizontal surface (there is a friction force) :

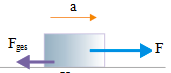∑F = m a

F – F_fric = m a

16 – 2 = 8 a

14 = 8 a

a = 14 / 8

a = 1.75 m/s²

Object’s acceleration is 1.75 m/s².

The correct answer is A.

10. Tom and Andrew push an object on the smooth floor. Tom push the object with a force of 5.70 N. If the mass of the object is 2.00 kg and acceleration experienced by the object is 2.00 ms^-2, then determine the magnitude and direction of force act by Tom.

A. 1.70 N and its direction is opposite with force acted by Andre.w

B. 1.70 N and its direction same as force acted by Andrew

C. 2.30 N and its direction is opposite with force acted by Andrew.

D. 2.30 N and its direction same as force acted by Andrew.

Known :

Push force acted by Andrew (F₁) = 5.70 Newton

Mass of object (m) = 2.00 kg

Acceleration (a) = 2.00 m/s²

Wanted : Magnitude and direction of force acted by Tom (F₂) ?

Solution :

Apply Newton’s second law of motion :

∑F = m a

F₁ + F₂ = m a

5.70 + F₂ = (2)(2)

5.70 + F₂ = 4

F₂ = 4 – 5.70

F₂ = – 1.7 Newton

Minus sign indicated that (F₂) is opposite with push force act by Andrew (F₁).

The correct answer is A.

11. If the mass of the block is the same, which figure shows the smallest acceleration?

Solution

Net force A :

ΣF = 4 N + 2 N – 3 N = 6 N – 3 N = 3 Newton, leftward

Net force B :

ΣF = 2 N + 3 N – 4 N = 5 N – 4 N = 1 Newton, rightward

Net force C :

ΣF = 4 N + 3 N – 2 N = 7 N – 2 N = 5 Newton, rightward

Net force D :

ΣF = 3 N + 4 N + 2 N = 9 Newton, rightward

The equation of Newton’s second law :

ΣF = m a

a = ΣF / m

a = acceleration, ΣF = net force, m = mass

Based on the above formula, the acceleration (a) is directly proportional to the net force (ΣF) and inversely proportional to mass (m). If the mass of an object is the same, the greater the resultant force, the greater the acceleration or the smaller the resultant force, the smaller the acceleration.
Based on the above calculation, the smallest net force is 1 Newton so the acceleration is also smallest.

The correct answer is B.

12. Some forces act on an object with a mass of 20 kg, as shown in the figure below.

Determine the object’s acceleration.

Known :

Mass of object (m) = 20 kg

Net force (ΣF) = 25 N + 30 N – 15 N = 40 N

Wanted: Acceleration of an object

Solution :

Object’s acceleration calculated using the equation of Newton’s second law :

ΣF = m a

a = ΣF / m = 40 N / 20 kg = 2 N/kg = 2 m/s²

13. Which statements below describes Newton’s third law?

(1) Passengers pushed forward when the bus braked suddenly

(2) Books on paper are not falling when the paper is pulled quickly

(3) When playing skateboard when the foot pushes the ground back then the skateboard will slide forward

(4) Oars pushed backward, boats moving forward

Solution :

(1) Newton’s first law

(2) Newton’s first law

(3) Newton’s third law

(4) Newton’s third law

[wpdm_package id=’470′]

1. Mass and weight
2. Normal force
3. Newton’s second law of motion
4. Friction force
5. Motion on the horizontal surface without friction force
6. The motion of two bodies with the same acceleration on the rough horizontal surface with the friction force
7. Motion on the inclined plane without friction force
8. Motion on the rough inclined plane with the friction force
9. Motion in an elevator
10. The motion of bodies connected by cord and pulley
11. Two bodies with the same magnitude of accelerations
12. Rounding a flat curve – dynamics of circular motion
13. Rounding a banked curve – dynamics of circular motion
14. Uniform motion in a horizontal circle
15. Centripetal force in uniform circular motion