Motion of two bodies with the same accelerations on the rough horizontal surface with the friction force – problems and solutions

1. Mass of the box 1 is 2 kg, the mass of the box 2 is 4 kg, acceleration of gravity is 10 m/s², the magnitude of the force F is 40 Newton. The coefficient of the kinetic friction between the box 1 with the floor is 0.2 and the coefficient of the kinetic friction between the box 2 and floor is 0.3. Find (a) The magnitude and direction of the box’s acceleration (b) Magnitude of the force exerted by the box 1 on the box 2 (F₁₂) and the magnitude of the force exerted by the box 2 on the box 1 (F₂₁).

Solution

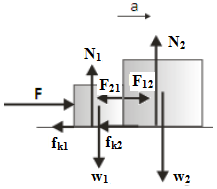
Known :

Mass of the box 1 (m₁) = 2 kg

Mass of the box 2 (m₂) = 4 kg

Acceleration of gravity (g) = 10 m/s²,

The force F = 40 Newton,

Coefficient of the kinetic friction between the box 1 with floor (μ_k1) = 0.2

Coefficient of the kinetic friction between the box 2 with floor (μ_k2) = 0.3

The weight of the box 1 (w₁) = m₁ g = (2)(10) = 20 Newton

The weight of the box 2 (w₂) = m₂ g = (4)(10) = 40 Newton

The normal force exerted on the box 1 (N₁) = w₁ = 20 Newton

The normal force exerted on the box 2 (N₂) = w₂ = 40 Newton

The force of the kinetic friction exerted on the box 1 (f_k1) = (μ_k1)(N₁) = (0.2)(20) = 4 Newton

The force of the kinetic friction exerted on the box 2 (f_k2) = (μ_k1)(N₂) = (0.3)(40) = 12 Newton

Solution :

(a) Magnitude and direction of the box’s acceleration

ΣF = m a

F – f_k1 – f_k2 = (m₁ + m₂) a

40 – 4 – 12 = (2 + 4) a

24 = 6 a

a = 24 / 6

a = 4 m/s²

Direction of the acceleration = direction of the net force = rightward.

(b) Magnitude of the force exerted by the box 1 on the box 2 (F₁₂) and the magnitude of the force exerted by the box 2 on the box 1 (F₂₁).

Calculate the magnitude of F₁₂ :

ΣF = m a

F₁₂ – f_k2 = (m₂) a

F₁₂ – 12 = (4)(4)

F₁₂ – 12 = 16

F₁₂ = 16 + 12

F₁₂ = 28 Newton

F₁₂ and F₂₁ are action and reaction forces that act on the different objects. F₁₂ and F₂₁ has the same magnitude and opposite direction.

F₁₂ = 28 Newton = F₂₁ = 28 Newton.

2. Mass of the box 1 is 2 kg, mass of the box 2 is 4 kg, acceleration of gravity is 10 m/s², the force F is 40 N. The coefficient of the kinetic friction between the box 1 with the floor is 0.2 and the coefficient of the kinetic friction between box 2 and floor is 0.3. Determine (a) Magnitude and direction of the acceleration (b) The tension in the cord connecting the boxes. Ignore cord’s mass.

Known :

Mass of the box 1 (m₁) = 2 kg

Mass of the box 2 (m₂) = 4 kg

Acceleration of gravity (g) = 10 m/s²,

The force F = 40 Newton,

Coefficient of the kinetic friction between the box 1 with floor is 0.2 (μ_k1) = 0.2

Coefficient of the kinetic friction between the box 2 with floor is 0.2 (μ_k2) = 0.3

The weight of the box 1 (w₁) = m₁ g = (2)(10) = 20 Newton

The weight of the box 2 (w₂) = m₂ g = (4)(10) = 40 Newton

The normal force exerted on the box 1 (N₁) = w₁ = 20 Newton

The normal force exerted on the box 2 (N₂) = w₂ = 40 Newton

The force of the kinetic friction exerted on the box 1 (f_k1) = (μ_k1)(N₁) = (0.2)(20) = 4 Newton

The force of the kinetic friction exerted on the box 2 (f_k2) = (μ_k1)(N₂) = (0.3)(40) = 12 Newton

Solution :

(a) magnitude and direction of the acceleration

ΣF = m a

F – f_k1 – f_k2 = (m₁ + m₂) a

40 – 4 – 12 = (2 + 4) a

24 = 6 a

a = 24 / 6

a = 4 m/s²

Magnitude of the acceleration is 4 m/s², direction of the acceleration = direction of the net force = rightward.

(b) Tension in the cord

Forces acts on the box 1 in the horizontal direction are the tension 1 (T₁) rightward and force of the kinetic friction 1 (f_k1) leftward. Apply Newton’s second law :

ΣF = m a

T₁ – f_k1 = m₁ a

T₁ – 4 = (2)(4)

T₁ – 4 = 8

T₁ = 8 + 4 = 12 Newton

The forces acts on the box 2 in the horizontal direction are the tension 2 (T₂) leftward and force of the kinetic friction 2 (f_k2) rightward. Apply Newton’s second law :

ΣF = m a

F – T₂ – f_k2 = m₂ a

40 – T₂ – 12 = (4)(4)

28 – T₂ = 16

T₂ = 28 – 16 = 12 Newton

The tension in the cord connecting the boxes = T₁ = T₂ = T = 12 Newton.

[wpdm_package id=’493′]

1. Mass and weight
2. Normal force
3. Newton’s second law of motion
4. Friction force
5. Motion on horizontal surface without friction force
6. Motion of two bodies with the same acceleration on rough horizontal surface with friction force
7. Motion on inclined plane without friction force
8. Motion on rough inclined plane with friction force
9. Motion in an elevator
10. Motion of bodies connected by cord and pulley
11. Two bodies with the same magnitude of accelerations
12. Rounding a flat curve – dynamics of circular motion
13. Rounding a banked curve – dynamics of circular motion
14. Uniform motion in a horizontal circle
15. Centripetal force in uniform circular motion