Carnot engine (application of the second law of thermodynamics) – problems and solutions

25 Carnot engine (application of the second law of thermodynamics) – problems and solutions

1. An engine operates between 1200 Kelvin and 300 Kelvin. What is the efficiency of this engine?

Known :

High temperature (T_H) = 1200 K

Low temperature (T_L) = 300 K

Wanted: Efficiency (e)

Solution :

2. An engine operates between 727^oC and 127^oC. The engine’s heat input is 6000 Joule. What is the efficiency of the engine and work done by the engine each cycle?

Known :

High temperature (T_H) = 727^oC + 273 = 1000 K

Low temperature (T_L) = 127^oC + 273 = 400 K

Heat input (Q_H) = 6000 Joule

Wanted: Efficiency (e) and work done by the engine (W)

Solution :

The efficiency of the Carnot engine :

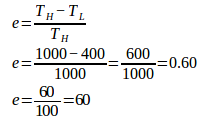
Work is done by the Carnot engine :

W = e Q_H

W = (0.6)(6000)

W = 3600 Joule

3. An engine operates between 527^oC and 127^oC. The engine’s heat input is 10,000 Joule. How much heat is discharged as waste heat from this engine?

Known :

High temperature (T_H) = 527^oC + 273 = 800 K

Low temperature (T_L) = 127^oC + 273 = 400 K

Heat input (Q_H) = 10,000 Joule

Wanted : Heat output (Q_L)

Solution :

Efficiency of the Carnot engine :

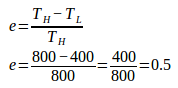
Work is done by Carnot engine :

W = e Q₁

W = (0.5)(10.000)

W = 5000 Joule

Heat output (Q_L) = Heat input (Q_H) – Work (W)

Q_L = Q_H – W

Q_L = 10,000 – 5,000

Q_L = 5000 Joule

4. What is the efficiency of the engine and work done by the engine according to diagram below.

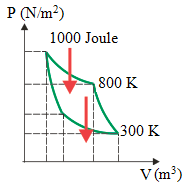Known :

High temperature (T_H) = 800 K

Low temperature (T_L) = 300 K

Heat input (Q_H) = 1000 Joule

Wanted: Efficiency (e) and work (W) done by the engine

Solution :

The efficiency of the Carnot engine :

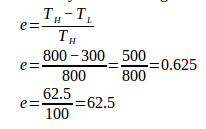
Work is done by the Carnot engine :

W = e Q_H

W = (0.625)(1000)

W = 625 Joule

5. If a Carnot engine operates between \( 500\,K \) and \( 300\,K \), calculate its efficiency.
Solution: \( \eta = 1 – \frac{T_C}{T_H} = 1 – \frac{300}{500} = 0.4 = 40\% \)

6. Find the efficiency of a Carnot refrigerator operating between \( 300\,K \) and \( 250\,K \).
Solution: \( \eta = \frac{T_C}{T_H – T_C} = \frac{250}{50} = 5 = 500\% \)

7. A Carnot engine’s efficiency is \( 30\% \). If \( T_C = 300\,K \), find \( T_H \).
Solution: \( T_H = \frac{T_C}{1 – \eta} = \frac{300}{0.7} \approx 428.57\,K \)

8. If a Carnot heat pump operates between \( 270\,K \) and \( 330\,K \), find the coefficient of performance (COP).
Solution: \( \text{COP} = \frac{T_H}{T_H – T_C} = \frac{330}{60} = 5.5 \)

9. Determine \( T_C \) for a Carnot engine with \( 50\% \) efficiency and \( T_H = 400\,K \).
Solution: \( T_C = T_H \times (1 – \eta) = 400 \times 0.5 = 200\,K \)

10. Calculate the efficiency of a Carnot engine operating between \( 373\,K \) and \( 273\,K \).
Solution: \( \eta = 1 – \frac{273}{373} \approx 0.268 = 26.8\% \)

11. Find the COP of a Carnot refrigerator with \( T_C = 260\,K \) and \( T_H = 300\,K \).
Solution: \( \text{COP} = \frac{T_C}{T_H – T_C} = \frac{260}{40} = 6.5 \)

12. A Carnot engine has \( 25\% \) efficiency and \( T_C = 200\,K \). Find \( T_H \).
Solution: \( T_H = \frac{T_C}{1 – \eta} = \frac{200}{0.75} \approx 266.67\,K \)

13. If a Carnot heat pump operates between \( 220\,K \) and \( 320\,K \), find the COP.
Solution: \( \text{COP} = \frac{T_H}{T_H – T_C} = \frac{320}{100} = 3.2 \)

14. Determine \( T_C \) for a Carnot engine with \( 60\% \) efficiency and \( T_H = 500\,K \).
Solution: \( T_C = T_H \times (1 – \eta) = 500 \times 0.4 = 200\,K \)

15. Calculate the efficiency of a Carnot engine operating between \( 600\,K \) and \( 400\,K \).
Solution: \( \eta = 1 – \frac{400}{600} \approx 0.333 = 33.3\% \)

16. Find the COP of a Carnot refrigerator with \( T_C = 280\,K \) and \( T_H = 330\,K \).
Solution: \( \text{COP} = \frac{T_C}{T_H – T_C} = \frac{280}{50} = 5.6 \)

17. A Carnot engine has \( 40\% \) efficiency and \( T_C = 250\,K \). Find \( T_H \).
Solution: \( T_H = \frac{T_C}{1 – \eta} = \frac{250}{0.6} \approx 416.67\,K \)

18. If a Carnot heat pump operates between \( 270\,K \) and \( 370\,K \), find the COP.
Solution: \( \text{COP} = \frac{T_H}{T_H – T_C} = \frac{370}{100} = 3.7 \)

15. Determine \( T_C \) for a Carnot engine with \( 75\% \) efficiency and \( T_H = 800\,K \).
Solution: \( T_C = T_H \times (1 – \eta) = 800 \times 0.25 = 200\,K \)

16. Calculate the efficiency of a Carnot engine operating between \( 700\,K \) and \( 300\,K \).
Solution: \( \eta = 1 – \frac{300}{700} \approx 0.571 = 57.1\% \)

17. Find the COP of a Carnot refrigerator with \( T_C = 250\,K \) and \( T_H = 350\,K \).
Solution: \( \text{COP} = \frac{T_C}{T_H – T_C} = \frac{250}{100} = 2.5 \)

18. A Carnot engine has \( 10\% \) efficiency and \( T_C = 150\,K \). Find \( T_H \).
Solution: \( T_H = \frac{T_C}{1 – \eta} = \frac{150}{0.9} \approx 166.67\,K \)

19. If a Carnot heat pump operates between \( 200\,K \) and \( 400\,K \), find the COP.
Solution: \( \text{COP} = \frac{T_H}{T_H – T_C} = \frac{400}{200} = 2 \)

20. Determine \( T_C \) for a Carnot engine with \( 80\% \) efficiency and \( T_H = 1000\,K \).
Solution: \( T_C = T_H \times (1 – \eta) = 1000 \times 0.2 = 200\,K \)