Materi Perkalian Titik Menggunakan Komponen Vektor Satuan
Kita dapat menghitung perkalian skalar secara langsung jika kita mengetahui komponen x, y dan z dari vektor A dan B (vektor yang diketahui).
Untuk melakukan perkalian titik dengan cara ini, terlebih dahulu kita lakukan perkalian titik dari vektor satuan, setelah itu kita nyatakan vektor A dan B dalam komponen-komponennya, menguraikan perkaliannya dan menggunakan perkalian dari vektor-vektor satuannya.
Vektor satuaj i, j dan k saling tegak lurus satu sama lain, sehingga memudahkan kita dalam perhitungan. Menggunakan persamaan perkalian skalar yang telah diturunkan di atas (A.B = AB cos teta) kita peroleh :
i . i = j . j = k . k = (1)(1) cos 0 = 1
i . j = i . k = j . k = (1)(1) cos 90o = 0
Sekarang kita nyatakan vektor A dan B dalam komponen-komponennya, menguraikan perkaliannya dan menggunakan perkalian dari vektor-vektor satuannya.
A . B = Axi . Bxi + Axi . Byj + Axi . Bzk +
Ayj . Bxi + Ayj . Byj + Ayj . Bzk +
Azk . Bxi + Azk . Byj + Azk . Bzk
A . B = AxBx (i . i) + AxBy (i . j) + Ax Bz (i . k) +
AyBx (j . i) + AyBy (j . j) + AyBz (j . k) +
AzBx (k . i) + AzBy (k . j) + AzBz (k . k)
Karena i . i = j . j = k . k = 1 dan i . j = i . k = j . k = 0, maka :
A . B = AxBx (1) + AxBy (0) + Ax Bz (0) +
AyBx (0) + AyBy (1) + AyBz (0) +
AzBx (0) + AzBy (0) + AzBz (1)
A . B = AxBx (1) + 0 + 0 +
0 + AyBy (1) + 0 +
0 + 0 + AzBz (1)
A . B = AxBx + AyBy + AzBz
Berdasarkan hasil perhitungan ini, bisa disimpulkan bahwa perkalian skalar atau perkalian titik dari dua vektor adalah jumlah dari perkalian komponen-komponennya yang sejenis.
Contoh Soal 1 :
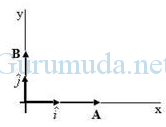Besar vektor A dan B berturut-turut adalah 5 dan 4, sebagaimana tampak pada gambar di bawah. Sudut yang terbentuk adalah 90o. Hitunglah perkalian titik kedua vektor.
Pembahasan
Sebelum kita menghitung perkalian titik vektor A dan B, terlebih dahulu kita ketahui komponen vektor kedua tersebut.
Ax = (5) cos 0o = (5) (1) = 5
Ay = (5) sin 0o = (5) (0) = 0
Az = 0
Bx = (4) cos 90o = (4) (0) = 0
By = (4) sin 90o = (4) (1) = 4
Bz = 0
Vektor A hanya mempunyai komponen vektor pada sumbu x dan vektor B hanya mempunyai komponen vektor pada sumbu y. Komponen z bernilai nol karena vektor A dan B berada pada bidang xy.
Sekarang kita hitung perkalian titik antara vektor A dan B menggunakan persamaan perkalian titik dengan vektor komponen :
A . B = Ax Bx + AyBy + AzBz
A . B = (5) (0) + (0) (4) + 0
A . B = 0 + 0 + 0
A . B = 0
Coba kita bandingkan dengan cara pertama
A.B = AB cos teta
A.B = (4)(5) cos 90
A.B = (4) (5) (0)
A.B = 0
Hasilnya sama.
Contoh Soal 2 :
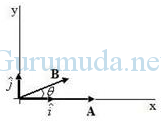Besar vektor A dan B berturut-turut adalah 5 dan 4, sebagaimana tampak pada gambar di bawah. Hitunglah perkalian titik kedua vektor tersebut, jika sudut yang terbentuk adalah 30o
Pembahasan
Sebelum kita menghitung perkalian titik vektor A dan B, terlebih dahulu kita ketahui komponen vektor kedua tersebut.
Komponen z bernilai nol karena vektor A dan B berada pada bidang xy.
Sekarang kita hitung perkalian titik antara vektor A dan B menggunakan persamaan perkalian titik dengan vektor komponen :
Bandingkan dengan cara pertama.
