Rolling motion – problems and solutions

1. A hollow cylindrical object (I = m R²) moves to roll without slipping up a rough inclined plane with an initial velocity of 10 m/s. The inclined plane has an elevation angle θ with tan θ = 0.75. If the gravitational acceleration g = 10 m.s^-2, the velocity of the object is reduced to 5 m.s^-1 then the distance on the inclined plane of the object is…

Known :

Moment of inertia of the hollow cylinder (I) = m R²

Elevation angle = θ, where tan θ = 0.75 = 75/100 = opp / adj

Sin θ = opp / hyp = 75/125 = 3/5 = 0.6

Acceleration due to gravity (g) = 10 m/s²

Initial velocity (v_o) = 10 m/s

Final velocity (v_t) = 5 m/s

Wanted : Distance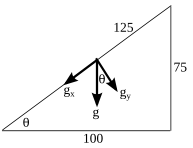

Solution :

Calculate the height reached by the cylinder using equation of the conservation of mechanical energy.

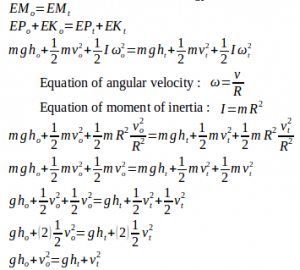
Initial height (h_o) = 0 meter

Initial velocity (v_o) = 10 m/s

Final velocity (v_t) = 5 m/s

Acceleration due to gravity (g) = 10 m/s²

The cylinder reaches a height of 7.5 meters.

Distance traveled by cylinder :

The distance traveled by the cylinder is 12.5 meters.

The correct answer is A.

Description of the equation :

_o = initial, _t = final, ME = mechanical energy, PE = potential energy, KE = kinetic energy, m = mass, g = acceleration due to gravity, h = height, v = linear velocity, ω = angular velocity, I = moment of inertia, R = radius of cylinder

2. A solid cylinder (I = ½ m R²) with a mass of 3 kg moves to roll without slipping up a rough inclined plane having an elevation angle θ with sin θ = 0.6. If the gravitational acceleration g = 10 m.s^-2 and the initial velocity of the object is 10 m/s, then the length of the inclined plane traveled by an object is…

Known :

Moment of inertia of solid cylinder (I) = ½ m R²

Mass of cylinder = 3 kg

Initial velocity (v_o) = 10 m/s

Final velocity (v_t) = 0 m/s (object stop)

Elevation angle (θ) = θ, where sin θ = 0.6 = 6/10 = opp/hyp

Acceleration due to gravity (g) = 10 m/s²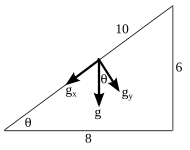

Wanted : The length of the inclined plane traveled by object

Solution :

Calculate the height reached by the cylinder using equation of the conservation of mechanical energy.

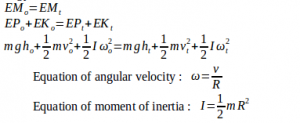
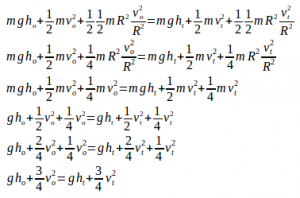
Initial height (h_o) = 0 meter

Initial velocity (v_o) = 10 m/s

Final velocity (v_t) = 0 m/s (object stop)

Acceleration due to gravity (g) = 10 m/s²

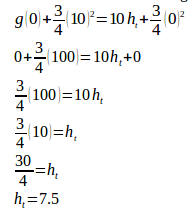
The cylinder reaches a height of 7.5 meters.

Distance traveled by cylinder :

The distance traveled by the cylinder is 12.5 meters.

3. A hollow cylindrical object (I = m R²) with radius R, moves to roll without slipping up a rough inclined plane with an angle of α where sin α = 0.8. If the gravitational acceleration g = 10 m.s^-2 and the initial velocity is 8 m.s^-1 then the length of the inclined plane reached by the object before it stops is…

Known :

Moment of inertia of solid cylinder (I) = m R²

Initial velocity (v_o) = 8 m/s

Final velocity (v_t) = 0 m/s (object stop)

Elevation angle of inclined plane (θ) = θ, where sin θ = 0.8

Acceleration due to gravity (g) = 10 m/s²

Wanted : Distance traveled by cylinder

Solution :

Calculate the height reached by the cylinder using equation of the conservation of mechanical energy.

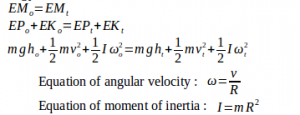
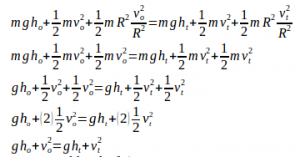
Initial height (h_o) = 0 meter

Initial velocity (v_o) = 8 m/s

Final velocity (v_t) = 0 m/s

Acceleration due to gravity (g) = 10 m/s²

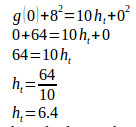
The cylinder reaches a height of 6.4 meters.

Distance traveled by cylinder :

The distance traveled by the cylinder is 8 meters.