Electrical energy in capacitor circuits – problems and solutions

Electrical energy in capacitor circuits – problems and solutions

1. Determine the electrical energy in the circuit shown in the figure below (1 µF = 10^-6 F)

Known :

Capacitor 1 (C₁) = 3 µF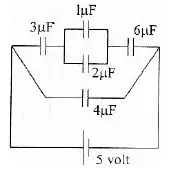

Capacitor 2 (C₂) = 1 µF

Capacitor 3 (C₃) = 2 µF

Capacitor 4 (C₄) = 6 µF

Capacitor 5 (C₅) = 4 µF

Electric voltage (V) = 5 volts

Wanted : Electrical energy in circuits

Solution :

The equivalent capacitor :

Capacitor 2 and capacitor 3 are connected in parallel. The equivalent capacitor :

C_A = C₂ + C₃ = 1 + 2 = 3 µF

Capacitor 1, capacitor A and capacitor 4 are connected in series. The equivalent capacitor :

1/C_B = 1/C₁ + 1/C_A + 1/C₄ = 1/3 + 1/3 + 1/6 = 2/6 + 2/6 + 1/6 = 5/6

C_B = 6/5 µF

Capacitor B and capacitor 5 are connected in parallel. The equivalent capacitor :

C = C_B + C₅ = 6/5 + 4 = 6/5 + 16/4 = 24/20 + 80/20 = 104/20 = 5.2 µF

C = 5.2 x 10^-6 Farad

Electrical energy in circuit :

E = ½ C V² = ½ (5.2 x 10^-6)(5²) = (2.6 x 10^-6)(25)

E = 65 x 10^-6 Joule

2. Determine the electrical energy in capacitor circuits shown in figure below (1 µF = 10^-6 F)

Known :

Capacitor 1 (C₁) = 4 µF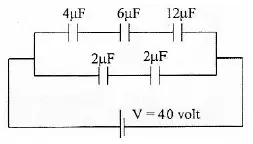

Capacitor 2 (C₂) = 6 µF

Capacitor 3 (C₃) = 12 µF

Capacitor 4 (C₄) = 2 µF

Capacitor 5 (C₅) = 2 µF

Electric voltage (V) = 40 volts

Wanted : Electrical energy in circuits

Solution :

The equivalent capacitor :

Capacitor 1, capacitor 2 and capacitor 3 are connected in series. The equivalent capacitor :

1/C_A = 1/C₁ + 1/C₂ + 1/C₃ = 1/4 + 1/6 + 1/12 = 3/12 + 2/12 + 1/12 = 6/12

C_A = 12/6 = 2 µF

Capacitor 4 and capacitor 5 are connected in series. The equivalent capacitor :

1/C_B = 1/C₄ + 1/C₅ = 1/2 + 1/2 = 2/2

C_B = 2/2 = 1 µF

Capacitor A and capacitor B in parallel. The equivalent capacitor :

C = C_A + C_B = 2 + 1 = 3 µF

C = 3 x 10^-6 Farad

Electrical energy in circuits :

E = ½ C V² = ½ (3 x 10^-6)(40²) = (1.5 x 10^-6)(1600)

E = 2400 x 10^-6 = 2.4 x 10^-3 Joule

3. Determine the energy stored in the electrical circuit shown in the figure below.

Known :

Capacitor 1 (C₁) = 4 F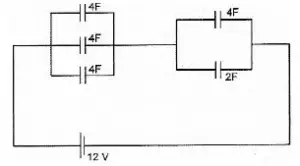

Capacitor 2 (C₂) = 4 F

Capacitor 3 (C₃) = 4 F

Capacitor 4 (C₄) = 4 F

Capacitor 5 (C₅) = 2 F

Electric voltage (V) = 12 volts

Wanted : Electrical energy in circuits

Solution :

The equivalent capacitor :

Capacitor 1, capacitor 2 and capacitor 3 are connected in parallel. The equivalent capacitor :

C_A = C₁ + C₂ + C₃ = 4 + 4 + 4 = 12 F

Capacitor 4 and capacitor 5 are connected in parallel. The equivalent capacitor :

C_B = C₄ + C₅ = 4 + 2 = 6 F

Capacitor A and capacitor B are connected in series. The equivalent capacitor :

1/C = 1/C_A + 1/C_B = 1/12 + 1/6 = 1/12 + 2/12 = 3/12

C = 12/3 = 4 Farad

Electrical energy in circuits :

E = ½ C V² = ½ (4)(12²) = (2)(144)

E = 288 Joule

1. Question: How is energy stored in a capacitor?

Answer: Energy in a capacitor is stored in the electric field between its plates. When a voltage is applied across a capacitor, positive charges accumulate on one plate and negative charges on the opposite plate, creating an electric field.

2. Question: What is the formula for the energy stored in a capacitor?

Answer: The energy (U) stored in a capacitor is given by �=12��2U=21​CV2 where C is the capacitance and V is the voltage across the capacitor.

3. Question: What happens to the energy stored in a capacitor when the voltage is doubled?

Answer: Since the energy is proportional to the square of the voltage (V^2), when the voltage is doubled, the energy increases by a factor of four.

4. Question: Why can a charged capacitor be dangerous even if it’s disconnected from its voltage source?

Answer: A charged capacitor can retain its stored energy even when disconnected from its voltage source. If a conductor (or a person) comes into contact with the terminals, the stored energy can be rapidly released, potentially causing harm or damage.

5. Question: How does the energy stored in a capacitor change if the capacitance is halved while keeping the voltage constant?

Answer: If the capacitance is halved and voltage remains constant, the energy stored will also be halved, as the energy is directly proportional to the capacitance.

6. Question: What role does the dielectric material play in a capacitor?

Answer: The dielectric material increases the capacitance of the capacitor by reducing the effective electric field between the plates and also prevents charge conduction between the plates.

7. Question: In a series capacitor circuit, how does the total capacitance compare to the individual capacitances?

Answer: In a series arrangement, the inverse of the total capacitance (1/C_total) is the sum of the inverses of the individual capacitances. This means the total capacitance in a series configuration is always less than the smallest capacitance in the series.

8. Question: How is the total capacitance calculated for capacitors connected in parallel?

Answer: For capacitors in parallel, the total capacitance is the sum of the individual capacitances.

9. Question: Why does a capacitor block direct current (DC) but allow alternating current (AC) to pass through?

Answer: A capacitor blocks DC because once it’s fully charged, no further current can flow. However, with AC, the voltage is continuously changing, causing the capacitor to charge and discharge, allowing an effective current to flow.

10. Question: What happens to a capacitor’s voltage if it is connected to a battery and then disconnected before reaching full charge?

Answer: The capacitor will retain the voltage it had at the moment of disconnection and won’t charge further unless connected back to a power source.