Youngs double-slit experiment – problems and solutions
1. d is the distance between 2 slits, L is the distance between the slit and the viewing screen, P2 is the distance between the second-order fringe and the center of the screen. Determine the wavelength of light (1 Å = 10-10 m).
Known :
Distance between two slits (d) = 1 mm = 1 x 10-3 m
Distance between slit and the viewing screen (L) = 1 m
Distance between the second-order fringe and the central fringe (P2) = 1 mm = 1 x 10-3 m
Order (n) = 2
Wanted : the wavelength of light (λ)
Solution :
The equation of double-slit interference (constructive interference) :
d sin θ = n λ
sin θ ≈ tan θ = P2 / L = (1 x 10-3) / 1 = 1 x 10-3 m
The wavelength of light :
λ = d sin θ / n
λ = (1 x 10-3)(1 x 10-3) / 2 = (1 x 10-6) / 2
λ = 0.5 x 10-6 m = 5 x 10-7 m
λ = 5000 x 10-10 m
λ = 5000 Å
2. Figure below shown result of a double-slit interference. Determine the wavelength of light (1 m = 1010 Å)
Known :
Distance between two slits (d) = 0.8 mm = 8 x 10-4 m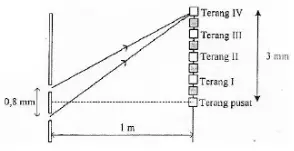
Distance between slit and the viewing screen (L) = 1 m
Distance between the fourth-order fringe and the central fringe (P) = 3 mm = 3 x 10-3 m
Order (n) = 4
Wanted : The wavelength of light (λ)
Solution :
The equation of double-slit interference (constructive interference) :
d sin θ = n λ
sin θ ≈ tan θ = P / L = (3 x 10-3) / 1 = 3 x 10-3 me
The wavelength of light :
λ = d sin θ / n
λ = (8 x 10-4)(3 x 10-3) / 4 = (24 x 10-7) / 4
λ = 6 x 10-7 m = 6000 x 10-10 m
λ = 6000 Å
3. Based on figure below, point A and B is the first two bright interference fringes and the wavelength of light is 6000 Å (1 Å = 10-10 m). Determine distance between two slits.
Known :
Distance between slit and the viewing screen (L) = 1 m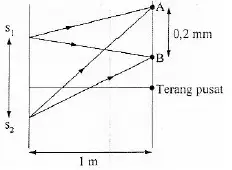
The wavelength of light (λ) = 6000 Å = 6000 x 10-10 m = 6 x 10-7 m
Distance between the first-order fringe and the central fringe (P) = 0.2 mm = 0.2 x 10-3 m = 2 x 10-4 m
Order (n) = 1
Wanted : Distance between two slits (d)
Solution :
The equation of constructive interference :
d = n λ / sin θ
sin θ ≈ tan θ = P / L = (2 x 10-4) / 1 = 2 x 10-4 m
Distance between two slits :
d = n λ / sin θ = (1)(6 x 10-7) / (2 x 10-4)
d = (6 x 10-7) / (2 x 10-4) = (3 x 10-3)
d = 0.003 m
d = 3 mm
10 problems related to Young’s double-slit experiment along with their solutions:
1. Problem: In a double-slit experiment, the interference pattern disappears when one of the slits is covered. Why?
Solution: When one slit is covered, the light can only pass through a single slit, which means there is no interference from two sources. This is why we see a single-slit diffraction pattern instead of the double-slit interference pattern.
2. Problem: The interference pattern shifts when a glass plate is placed in front of one of the slits. Why?
Solution: The glass plate introduces a phase change in the light wave passing through it. This phase change causes a relative path difference between the light waves coming from the two slits, thus shifting the interference pattern.
3. Problem: The distance between the interference fringes decreases as the wavelength of light used is increased. Explain.
Solution: The fringe spacing � is given by �=��� where � is the wavelength, � is the distance from the slits to the screen, and � is the distance between the slits. As � increases, � also increases.
4. Problem: When monochromatic red light is replaced by monochromatic blue light, the fringe spacing decreases. Why?
Solution: Blue light has a shorter wavelength than red light. As fringe spacing Δ� is directly proportional to � (wavelength), a shorter � will result in a smaller Δ�.
5. Problem: The interference pattern is not observed when the distance between the two slits is too large. Why?
Solution: For observable interference patterns, the path difference must be on the order of the wavelength of light. If the slits are too far apart, the angle at which constructive or destructive interference occurs becomes too small to differentiate between fringes.
6. Problem: The interference pattern disappears when the light source is too broad or incoherent. Why?
Solution: For interference to occur, the light waves must be coherent, meaning they maintain a consistent phase relationship. Broad or incoherent sources produce light waves with random phase relationships, eliminating the clear interference pattern.
7. Problem: The interference pattern shifts when the apparatus is immersed in water. Explain.
Solution: Immersing the apparatus in water changes the speed of light. The wavelength of light in water is reduced compared to air. As fringe spacing Δ� is directly proportional to �, the interference pattern shifts.
8. Problem: A student observes a blurred interference pattern. What could be the reasons?
Solution: The blurring can be due to several reasons: the slits might not be truly parallel, the screen might not be perfectly perpendicular to the light path, or the light source may not be perfectly monochromatic or coherent.
9. Problem: The fringes are not equally spaced. Why?
Solution: This could be due to non-uniformities in the slit widths or a non-linear spacing between the slits. Imperfections in the experimental setup can lead to uneven fringes.
10. Problem: The interference pattern is not observed at all when white light is used, but a central bright fringe is seen. Explain.
Solution: White light is composed of multiple colors (wavelengths) of light. Each color will interfere at different positions due to their different wavelengths. Overlapping of these patterns will wash out the distinct interference pattern, leaving only a central white fringe where all colors constructively interfere.
Note: The above problems and solutions are presented in a simplified manner for easier understanding. In real experiments, additional factors might play a role in the observations.
