Stress Strain Young’s modulus – Problems and Solutions

Stress Strain Young’s modulus – Problems and Solutions

1. A nylon string has a diameter of 2 mm, pulled by a force of 100 N. Determine the stress!

Known :

Force (F) = 100 N

Diameter (d) = 2 mm = 0.002 m

Radius (r) = 1 mm = 0.001 m

Wanted : The stress

Solution :

Area :

A = π r²

A = (3.14)(0.001 m)² = 0.00000314 m²

A = 3.14 x 10^-6 m²

The stress :

2. A cord has original length of 100 cm is pulled by a force. The change in length of the cord is 2 mm. Determine the strain!

Known :

Original length (l₀) = 100 cm = 1 m

The change in length (Δl) = 2 mm = 0.002 m

Wanted : The strain

Solution :

The strain :

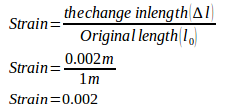
3. A string 4 mm in diameter has original length 2 m. The string is pulled by a force of 200 N. If the final length of the spring is 2.02 m, determine : (a) stress (b) strain (c) Young’s modulus

Known :

Diameter (d) = 4 mm = 0.004 m

Radius (r) = 2 mm = 0.002 m

Area (A) = π r² = (3.14)(0.002 m)²

Area (A) = 0.00001256 m² = 12.56 x 10^-6 m²

Force (F) = 200 N

Original length of spring (l₀) = 2 m

The change in length (Δl) = 2.02 – 2 = 0.02 m

Wanted : (a) The stress (b) The strain c) Young’s modulus

Solution :

(a) The stress

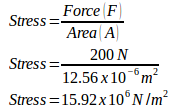
(b) The Strain

(c) Young’s modulus

4. A string has a diameter of 1 cm and the original length of 2 m. The string is pulled by a force of 200 N. Determine the change in length of the string! Young’s modulus of the string = 5 x 10⁹ N/m²

Known :

Young’s modulus (E) = 5 x 10⁹ N/m²

Original length (l₀) = 2 m

Force (F) = 200 N

Diameter (d) = 1 cm = 0.01 m

Radius (r) = 0.5 cm = 0.005 m = 5 x 10^-3 m

Area (A) = π r² = (3.14)(5 x 10^-3 m)² = (3.14)(25 x 10^-6 m²)

Area (A) = 78.5 x 10^-6 m² = 7.85 x 10^-5 m²

Wanted : The change in length (Δl)

Solution :

Young’s modulus formula :

The change in length :

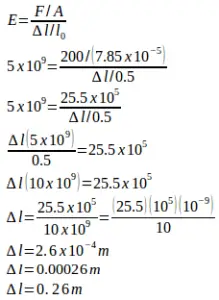
5. A concrete has a height of 5 meters and has unit area of 3 m³ supports a mass of 30,000 kg. Determine (a) The stress (b) The strain (c) The change in height! Acceleration due to gravity (g) = 10 m/s². Young’s modulus of concrete = 20 x 10⁹ N/m²

Known :

Young’s modulus of concrete = 20 x 10⁹ N/m²

Initial height (l₀) = 5 meters

Unit area (A) = 3 m²

Weight (w) = m g = (30,000)(10) = 300,000 N

Wanted : (a) The stress (b) The strain (c) The change in height!

Solution :

(a) The stress

(b) The Strain

(c) The change in height

1. Hooke’s law
2. Stress, strain, Young’s modulus