1. Based on the figure below, determine the electric current through R1.
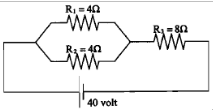Known :
Resistor 1 (R1) = 4 Ω
Resistor 2 (R2) = 4 Ω
Resistor 3 (R3) = 8 Ω
Electric voltage (V) = 40 Volt
Wanted: Electric current through R1
Solution :
The electric current flows from high potential to low potential. The direction of electric current in the circuit above is the same as a clockwise direction.
The electric current that flows out of the battery
First, calculate the equivalent resistance (R). Thereafter, calculate the electric current using the equation of Ohm’s law :
V = I R or I = V / R
V = voltage, I = electric current, R = the equivalent resistance
The equivalent resistance :
Resistor R1 and resistor R2 are connected in parallel. The equivalent resistance :
1/R12 = 1/R1 + 1/R2 = 1/4 + 1/4 = 2/4
R12 = 4/2 = 2 Ω
Resistor R12 and resistor R3 are connected in series. The equivalent resistance :
R = R12 + R3 = 2 + 8 = 10 Ω
The electric current that flows out of the battery :
I = V / R = 40 / 10 = 4 A
The electric current that flows out of the battery is 4 Ampere.
Electric voltage Vab and Vbc
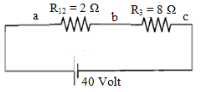Kirchhoff‘s first rule states that at any junction point, the sum of all currents entering the junction must equal the sum of all currents leaving the junction.
Based on Kirchhoff’s first rule, concluded that if the electric current flows out of the battery is 4 A then the electric current through a-b is equal to 4 Ampere, so also the electric current through b-c is 4 Ampere.
Electric voltage Vab :
Vab = Iab Rab = (4)(2) = 8 Volt
Electric voltage Vbc :
Vbc = Ibc Rbc = (4)(8) = 32 Volt
The above circuit is connected in series so that the total electrical voltage is V = Vab + Vbc = 8 Volt + 32 Volt = 40 Volt.
The electric current flows through R1 = 4 Ω
I1 = Vab / R1 = 8 Volt / 4 Ohm = 2 A
I2 = Vab / R2 = 8 Volt / 4 Ohm = 2 A
The electric current that flows out of the battery is 4 A. When it arrives at point a the electric current is divided into two, the electric current of 2 Ampere flows through the resistor R1 and
the electric current of 2 A flows through the resistor R2. 2 A + 2 A = 4 A.
2. Based on the figure below, determine the electric current that flows through resistor 4-Ω.
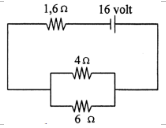Known :
Resistor 1 (R1) = 6 Ω
Resistor 2 (R2) = 4 Ω
Resistor 3 (R3) = 1.6 Ω
The electric voltage (V) = 16 Volt
Wanted: The electric current flows through 4 Ω
Solution :
The electric current flows from high potential to low potential. The direction of electric current in the circuit above is the same as a clockwise direction.
The electric current that flows out of the battery
The equivalent resistance :
Resistor R1 and resistor R2 are connected in parallel. The equivalent resistor :
1/R12 = 1/R1 + 1/R2 = 1/6 + 1/4 = 2/12 + 3/12 = 5/12
R12 = 12/5 = 2.4 Ω
Resistor R12 and resistor R3 are connected in series. The equivalent resistor :
R = R12 + R3 = 2.4 + 1.6 = 4 Ω
The electric current that flows out of the battery :
I = V / R = 16 / 4 = 4 A
The electric voltage Vab and Vbc
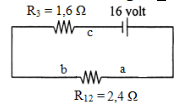Based on Kirchhoff’s first rule, concluded that if the electric current flows out of the battery is 4 A then the electric current through a-b is equal to 4 Ampere, so also the electric current through b-c is 4 Ampere.
The electric voltage Vab :
Vab = Iab Rab = (4)(2.4) = 9.6 Volt
The electric voltage Vbc :
Vbc = Ibc Rbc = (4)(1.6) = 6.4 Volt
The above circuit is connected in series so that the total electric voltage is V = Vab + Vbc = 9.6 Volt + 6.4 Volt = 16 Volt.
The electric current that flows through R2 = 4 Ω
I1 = Vab / R1 = 9.6 Volt / 6 Ohm = 1.6 A
I2 = Vab / R2 = 9.6 Volt / 4 Ohm = 2.4 A
The electric current that flows out of the battery is 4 A. When it arrives at point a the electric current is divided into two,
the electric current 1.6 A flows through the resistor R1 and the electric current 2.4 A flows through the resistor R2. 1.6 A + 2.4 A = 4 A.
