1. Four capacitors, C1 = 2 μF, C2 = 1 μF, C3 = 3 μF, C4 = 4 μF, are connected in series. Determine the capacitance of a single capacitor that will have the same effect as the combination.
Known :
Capacitor C1 = 2 μF
Capacitor C2 = 1 μF
Capacitor C3 = 3 μF
Capacitor C3 = 4 μF
Wanted : The equivalent capacitance
Solution :
The equivalent capacitance :
1/C = 1/C1 + 1/C2 + 1/C3 + 1/C4
1/C = 1/2 + 1/1 + 1/3 + 1/4
1/C = 6/12 + 12/12 + 4/12 + 3/12
1/C = 25/12
C = 12/25
C = 0.48
The equivalent capacitance of the entire combination is 0.48 μF.
2. Determine the charge on capacitor C1 if the potential difference between P and Q is 12 Volt…
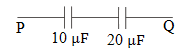Known :
Capacitor C1 = 10 μF = 10 x 10-6 F
Capacitor C2 = 20 μF = 20 x 10-6 F
Potential difference (V) = 12 Volt
Wanted : the charge on capacitor C1 (Q1)
Solution :
The equivalent capacitance :
1/C = 1/C1 + 1/C2
1/C = 1/10 + 1/20 = 2/20 + 1/20 = 3/20
C = 20/3 μF = (20/3) x 10-6 F
Electric charge on the equivalent capacitor :
Q = (C)(V) = (20/3)(12)(10-6) = 80 x 10-6 C
Q = 80 μC
Capacitors are connected in series so that electric charge on the equivalent capacitors = electric charge on capacitor C1 = electric charge on capacitor C2.
The electric charge on capacitor C1 is 80 μC.
3. Two capacitors, C1 = 2 μF and C2 = 4 μF, are connected in series. The capacitors are charged. The potential difference on capacitor C1 is 2 Volt. The electric charge on capacitor C2 is…
Known :
Capacitor C1 = 2 μF = 2 x 10-6 F
Capacitor C2 = 4 μF = 4 x 10-6 F
The potential difference on capacitor C1 (V1) = 2 Volt
Wanted : Electric charge on capacitor C2.
Solution :
Electric charge on capacitor C1 :
Q1 = C1 V1 = (2 x 10-6)(2) = 4 x 10-6 C
Q1 = 4 μC
Capacitors are connected series so that electric charge on capacitor C1 = electric charge on capacitor C2.
The charge on capacitor C2 is 4 μC.
