Particles in two-dimensional equilibrium – application of Newton’s first law problems and solutions

1. Find the tension force T₁, T₂, and T₃. Ignore cord’s mass.

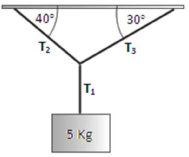
Solution

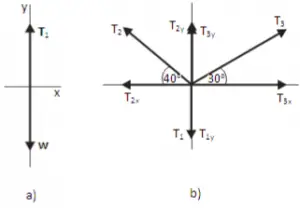
(a) Free-body diagram for object (b) Free-body diagram for cord

Apply the Newton’s first law on the object :

ΣF_y = 0

T₁ – w = 0

T₁ = w = m g

T₁ = (5 kg)(9.8 m/s²)

T₁ = 49 kg m/s²

T₁ = 49 N

Apply Newton’s first law on the cord :

∑F_x = 0

T_3x – T _2x = 0

T₃ cos 30^o – T₂ cos 40^o = 0

0.87 T₃ – 0.77 T₂ = 0

0.87 T₃ = 0.77 T₂

T₂ = 0.87 T₃ / 0.77 = 1.1 T₃ ———- Equation 1

——

∑F_y = 0

T_3y + T_2y – T_1y = 0

T₃ sin 30^o + T₂ sin 40^o – T₁ = 0

0.5 T₃ + 0.64 T₂ – 49 N = 0 ———- Equation 2

Substituting T₂ in the equation 2 into the equation 2 :

0.5 T₃ + 0.64 (1.1 T₃) – 49 N = 0

0.5 T₃ + 0.70 T₃ – 49 = 0

1.2 T₃ – 49 = 0

1.2 T₃ = 49

T₃ = 49 / 1.2

T₃ = 41 N

———

T₂ = 1.1 T₃

T₂ = (1.1)(40.8 N)

T₂ = 45 N

[wpdm_package id=’488′]

1. Particles in one-dimensional equilibrium
2. Particles in two-dimensional equilibrium
3. Equilibrium of bodies connected by cord and pulley
4. Equilibrium of bodies on inclined plane