Nearsighted and farsighted – problems and solutions
1. A child with nearsighted can read a book at a near point 1 meter. In order to read at a normal reading distance of 25 cm, determine the power of the lens must use by the child.
Solution :
The child suffers farsighted, where the near point of his eyes is 1 meter or 100 cm. The near point of the normal eye is 25 cm. The eye can normalize by a convex lens.
Known :
Near point = image distance (s’) = -100 cm
The shadow must be in front of the convex lens so it can be seen. Because the shadow is in front of the convex lens then the image is virtual and signed negative.
Normal reading distance = object distance (s) = 25 cm
Wanted : power of lens
Solution :
The focal length of the convex lens (f) :
1/f = 1/s + 1/s’ = 1/25 – 1/100 = 4/100 – 1/100 = 3/100
f = 100/3 cm
f = (100/3 : 100) m
f = (100/3 x 1/100) m
f = 1/3 m
The power of convex lens (P) :
P = 1 /f = 1 : 1/3 = 1 x 3/1 = 3 Diopters.
Power of convex lens is 3 diopters.
2.
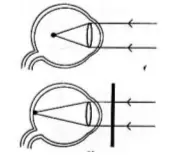
Based on the above figure, determine the eye defect used to normalized the eye.
Solution
Eye defects: farsighted
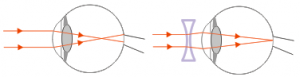
The light beam can be focused precisely on the retina when a concave lens is placed in front of the eye. Divergent lenses help spread the beam of light so that it can be focused precisely on the retina.
3. Someone can read at the closest distance of 50 cm. In order for him to read at a distance of 30 cm, determine the power of the eyeglasses lens.
Solution :
The person is suffering from nearsighted, the lenses used to normalize nearsighted eyes are convex lenses or convergent lenses or positive lenses.
In order for the observed object to be 30 cm in front of the eye, the lens should form an image at a distance of 50 cm in front of the eye. The image is in front of the lens so that the image is upright and virtual.
Known :
Object’s distance (s) = 30 cm
Image’s distance (s’) = -50 cm (negative because virtual)
Wanted : Power of lens (P)
Solution :
Focal length :
1/f = 1/s + 1/s’
1/f = 1/30 + 1/-50
1/f = 5/150 – 3/150
1/f = 2/150
f = 150/2 = 75 cm = 0.75 meter = 75/100 meters
Focal length signed positive means the lens used is convex lens.
Power of lens :
P = 1/f
P = 1 : 75/100 = 1 x 100/75
P = 100/75
P = 4/3 Diopters
