Kirchhoff’s second rule states that the change in electric potential on the circumference of a closed circuit is zero. Kirchhoff’s second rule is based on the law of conservation of energy, which states that energy is eternal.
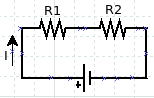To better understand this, imagine the electric charge moving in a closed circuit, as in the figure. When an electric charge passes through an electrical resistance (R), the electrical potential energy is reduced because it is used on these resistances. If the electric charge passes through another electrical resistance, the electric potential energy decreases again because it is used again on the resistance. Furthermore, when the electric charge passes through the voltage source from a low potential to a high potential, the electric potential energy increases. When it returns to its original point, the electric potential energy is the same as before, where the change in electrical potential energy is zero. When applying Kirchhoff‘s second rule to an electrical circuit, we use the change in electrical voltage, not the change in electrical potential energy.
The circuit as in the figure above can be analyzed using Ohm’s law (V = I R) and the equation for series resistance or parallel resistance. More complex circuits such as the figure can be analyzed using Kirchhoff’s first rule and Kirchhoff’s second rule.
Here are some significant rules when using Kirchhoff’s second rule to analyze a circuit.
First, choose the current direction, whether clockwise or counterclockwise. If the answer is negative, the actual direction of the electric current is in the direction of the current decided. If the answer is positive, the actual direction of the electric current is the same as the direction of the selected current.
Second, when passing through a voltage source from a high potential to a low potential (to -), there is a decrease in electrical voltage so that the voltage is negative (ΔV = -ε). Conversely, if it moves from a low potential to a high potential (- to), there is an increase in electrical voltage so that the voltage is positive (ΔV = ε).
Third, when it goes through electrical resistance, if the loop is in the direction of the electric current, the voltage is negative (V = – I R). Conversely, if the loop direction is opposite to the direction of the electric current, the electric voltage is positive (ΔV = I R).
Sample problem 1:
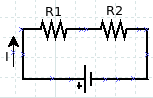R1 = 200 Ω and R2 = 300 Ω. ε = 12 Volt. Calculate the electric current flowing in the circuit using Kirchhoff‘s second rule!
Solution:
The direction of the clockwise direction.
– I R1 – I R2 + ε = 0
– 200 I – 300 I + 12 = 0.
– 500 I + 12 = 0
– 500 I = – 12
I = 12 / 500
I = 0.024 A
If calculated using Ohm’s law and the formula for the combination of resistors in series:
R = R1 + R2 = 200 + 300 = 500 Ω.
Equation of Ohm’s law:
V = I R
I = V / R = 12 / 500 = 0.024 A.
Sample problem 2:
R1 = 100 Ω, R2 = 200 Ω, R3 = 300 Ω, ε1 = 9 Volt, ε2 = 12 Volt. Calculate the magnitude and direction of the electric current in the circuit!
Solution:
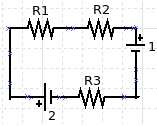Select the direction of electric current and the direction of the loop is the same as the clockwise direction.
– I R1 – I R2 – ε1 – I R3 + ε2 = 0
– 100 I – 200 I – 9 – 300 I + 12 = 0
– 100 I – 200 I – 300 I + 3 = 0
– 600 I + 3 = 0
– 600 I = – 3
I = 3 / 600
I = 0.005 A
Electric current is positive so that the direction is the same as the direction chosen.
