Kinetic theory of gases – problems and solutions

1. Ideal gases in a closed container initially have volume V and pressure P. If the final pressure is 4P and the volume is kept constant, what is the ratio of the initial kinetic energy with the final kinetic energy.

Known :

Initial pressure (P₁) = P

Final pressure (P₂) = 4P

Initial volume (V₁) = V

Final volume (V₂) = V

Wanted: The ratio of the initial kinetic energy with the final kinetic energy (KE₁ : KE₂)

Solution :

The relation between pressure (P), volume (V) and kinetic energy (KE) of ideal gases :

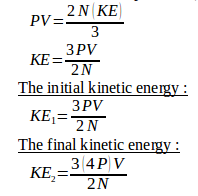
The ratio of the initial kinetic energy with the final kinetic energy :

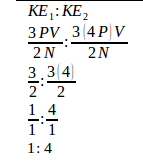
2. What is the average translational kinetic energy of molecules in an ideal gas at 57^oC.

Known :

Temperature of gas (T) = 57^oC + 273 = 330 Kelvin

Boltzmann‘s constant (k) = 1.38 x 10^-23 Joule/Kelvin

Wanted: The average translational kinetic energy

Solution :

The relation between kinetic energy (KE) and the temperature of the gas (T) :

The average translational kinetic energy :

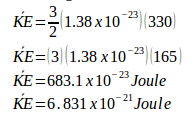
3. A gas at 27^oC in a closed container. If the kinetic energy of the gas increases 2 times the initial kinetic energy, thus the final temperature of the gas is…

Known :

Initial temperature (T₁) = 27^oC + 273 = 300 K

Initial kinetic energy = KE

Final kinetic energy = 4 KE

Wanted: The final temperature (T₂)

Solution :

4. An ideal gas is in a closed container, is heated so that the final average velocity of particles of gas increases by 3 times the initial average velocity. If the initial gas temperature is 27^oC, then the final temperature of the ideal gas is…

Known :

Initial temperature = 27^oC + 273 = 300 Kelvin

Initial velocity = v

Final velocity = 2v

Wanted : The final temperature of ideal gas

Solution :

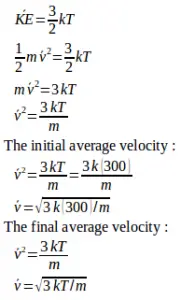
The final average velocity = 2 x the initial average velocity

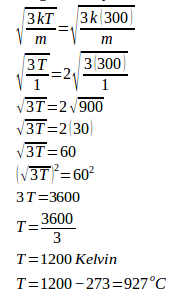
5. Three moles of gas are in a 36 liters volume space. Each gas molecule has a kinetic energy of 5 x 10^-21 Joule. Universal gas constant = 8.315 J/mole.K and Boltzmann’s constant = 1.38 x 10^-23 J/K. What is the gas pressure in the container.

Known :

Number of moles (n) = 3 moles

Volume = 36 liters = 36 dm³ = 36 x 10^-3 m³

Boltzmann’s constant (k) = 1.38 x 10^-23 J/K

Kinetic energy (KE) = 5 x 10^–21 Joule

Universal gas constant (R) = 8.315 J/mole.K

Wanted : Gas pressure (P)

Solution :

Calculate the temperature using the equation of kinetic energy of gas.

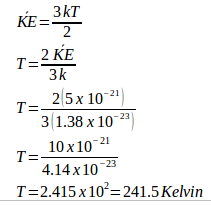
Calculate the gas pressure using th equation of ideal gas law (in number of moles, n) :

P V = n R T

P (36 x 10^-3) = (3)(8.315)(241.5)

P (36 x 10^-3) = 6024.22

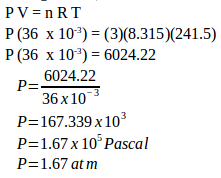
The gas pressure is 1.67 x 10⁵ Pascal or 1.67 atmospheres.