The specific statements of the second law of thermodynamics can’t describe for all irreversible processes, so we need a general statement. This general statement is expected to explain all irreversible processes occurring in the universe. The general statement of the second law of thermodynamics was formulated in the mid-nineteenth century, through a quantity called entropy (S). Entropy was first introduced by Clausius and was formulated from the Carnot cycle (perfect caloric engine). According to Clausius, entropy changes are experienced by a system, when the system gets additional heat (Q) at a constant temperature, which is represented by the equation:
ΔS = Entropy changes, Q = Heat, T = Temperature
Entropy is a quantity that states the microscopic state of the system so that it cannot be known directly. Which can be calculated only entropy changes. Much like an internal energy change in the first law of thermodynamics.
Example 1:
The gas in the container expands adiabatically. The change in gas entropy is…
Solutions
During the adiabatic process, no heat enters or exits the system (gas). Since Q = 0 then ΔS = 0. The system entropy is constant. What about adiabatic compression? During adiabatic compression, no heat enters or leaves the system (Q = 0). Therefore, the entropy of the system is constant.
Example 2:
The Carnot engine absorbs the heat of 2000 J at 500 K, releases heat at 350 K. Calculate the heat released, and the change in total entropy for one cycle.
Solutions
TH = 500 K
QH = 2000 J
TL = 350 K
QL = ….. ?
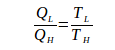
If the system receives heat, Q is positive, if the system releases heat, Q is negative.
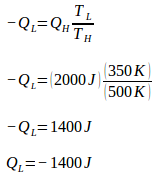
During one cycle, the Carnot engine undergoes two reversible isothermal processes (isothermal expansion + isothermal compression) and two reversible adiabatic processes (adiabatic expansion and adiabatic compression). During expansion and compression, no heat enters or leaves the system (Q = 0). Since Q = 0, entropy changes during the adiabatic process = 0.
During isothermal expansion, the engine absorbs heat (Q) of 2000 J at a temperature (T) 500 K. Because the engine absorbs heat, then Q is positive. The change of machine entropy during isothermal expansion is:
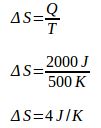During isothermal compression, the engine releases heat (Q) as much as 1400 J at a temperature of (T) 350 K. Because the machine releases heat, then Q is negative. The change of machine entropy during isothermal presses is:
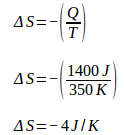
Total entropy change = 4 J / K – 4 J / K = 0
Example 3:
The engine absorbs 600 J of heat at a temperature of 300 °C, releases heat at a temperature of 100 °C. Calculates the heat that is released, and changes in total entropy for one cycle
Solutions
TH = 300 K
QH = 600 J
TL = 100 K
QL = ?
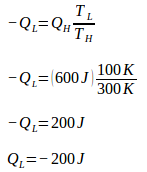
During one cycle, the Carnot engine undergoes two reversible isothermal processes (isothermal expansion + isothermal compression) and two reversible adiabatic processes (adiabatic compression and adiabatic expansion). During adiabatic expansion and compression, no heat enters or leaves the system (Q = 0). Because Q = 0 then the entropy change during the adiabatic process = 0.
During isothermal expansion, the engine absorbs heat (Q) of 600 J at a temperature of (T) 300 K. Because the engine absorbs heat, then Q is positive. The change of machine entropy during isothermal expansion is:
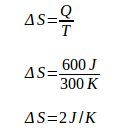
During isothermal compression, the engine releases heat (Q) 200 J at a temperature (T) 100 K. Because the engine releases heat, then Q is negative. The change of machine entropy during isothermal compression is:
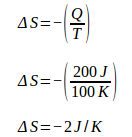
Total entropy change = 2 J / K – 2 J / K = 0
Based on example number 2 and example number 3, the total entropy change for the reversible process = 0. In the reversible process, the total entropy is always constant.
Example 4 :
Ice 2 kg at 0 °C absorbs heat, so it melts. Calculate the change in ice entropy. (The heat of fusion for water = 3.34 x 105 J / Kg)
Solutions
Ice mass = 2 kg
Ice temperature = 0 oC + 273 = 273 K
The heat of fusion for water = 3.34 x 105 J / Kg
The heat needed to melt 2 kg of ice into water:
Q = mL
Q = (2 kg)(3.34 x 105 J/Kg)
Q = 6.68 x 105 J
Q = 668 x 103 J
During the melting process (ice to water), the temperature is constant. Since the temperature is constant, then the change of ice entropy is :
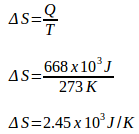
Example 5:
Water at 26 °C is mixed with water at 22 °C. The water mass is 2 kg. Calculate the change in water entropy. Hot water and cold water are mixed in a well-insulated, closed container. Heat transfer is an irreversible process.
Solutions
Specific heat of water (c) = 4180 J/Kg Co
Water mass = 2 Kg
The water mass is the same, so the final temperature = 24 oC (26 oC + 22 oC / 2 = 48 oC / 2 = 24 oC).
The amount of heat that is released by hot water when the temperature is reduced from 26 °C – 24 °C is :
Q = m c ΔT = (2 kg) (4180 J / kg Co) (26 oC – 24 oC) = (2 Kg) (4180 J / kg Co) (2 oC) = 16720 J
The amount of heat that is absorbed by cold water when the temperature rises from 22oC – 24oC is :
Q = m c ΔT = (2 kg) (4180 J / kg Co) (24 oC – 22 oC) = (2 kg) (4180 J / kg Co) (2 oC) = 16720 J
Total entropy change = hot water entropy change + cold water entropy change
ΔS = ΔS hot water + ΔS cold water
ΔS = Q/T + Q/T
Average temperature of hot water = (26 oC + 24 oC) / 2 = 50 oC / 2 = 25 oC —- 25 + 273 = 298 K
Average temperature of cold water = (22 oC + 24 oC) / 2 = 46 oC / 2 = 23 oC —- 23 + 273 = 296 K
Hot water releases heat, so Q is negative. Cold water absorbs heat, so Q is positive.
ΔS = ΔS hot water + ΔS cold water
ΔS = -Q/T + Q/T
ΔS = -16720/298 + 16720/296
ΔS = -56.107 + 56.486
ΔS = 0.379 J/K
Total entropy increased by 0.379 J / K
Although the partial entropy of the system decreases (-56.107 J/K), the partial entropy of the system increases in larger quantities (+ 56.486 J / K) so that total entropy is always increased (+ 0.379 J / K).
The increase in total entropy in the irreversible process is not only applicable to heat transfer between hot and cold water mixtures analyzed above, but also applies to all cases examined by scientists. Total fixed entropy if the process occurs reversibly. If the process occurs irreversibly, then total entropy always increases.
All natural processes in our daily life are irreversible so that total entropy must increase. This fact is summarized in the following sentence:
In an irreversible process, the total entropy of the system and the environment is always growing.
This statement is a general statement of the second law of thermodynamics. The second law of thermodynamics is different from other physical laws. Usually, the laws of physics are expressed regarding equations (Newton’s law) or in the form of the law of eternity (the law of conservation of energy).
