Temperature and heat – problems and solutions
1. On a thermometer X, the freezing point of water at -30o and the boiling point of water at 90o. 60OX = ….. oC.
Known :
The freezing point of water = -30o
The boiling point of water = 90o
Wanted : 60oX = ….. oC
Solution :
On the Fahrenheit scale, the freezing point of water is 32oF and the boiling point of water is 212oF. Between the freezing point and the boiling point, 212o – 32o = 180o.
On the Celsius scale, the freezing point of water is 0oC and the boiling point of water is 100oC. Between the freezing point and the boiling point, 100o – 0o = 100o.
On the X scale, the freezing point of water is -30oX and the boiling point of water is 90oX. Between the freezing point and the boiling point, 90o – (-30o) = 90o + 30o = 120o.
Change the X scale to the Celsius scale :
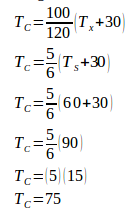
2. A metal rod heated from 30oC to 80oC. The final length of the rod is 115 cm. The coefficient of linear expansion is 3.10-3 oC-1. What is the initial length of the metal rod?
Known :
The initial temperature (T1) = 30oC
The final temperature (T2) = 80oC
The change in temperature (ΔT) = 80oC – 30oC = 50oC
The coefficient of linear expansion (α) = 3.10-3 oC-1
The final length of the metal (L) = 115 cm
Wanted : The initial length of the metal rod (Lo)
Solution :
The equation of the linear expansion :
L = Lo + ΔL
L = Lo + α Lo ΔT
L = Lo (1 + α ΔT)
115 = Lo (1 + 3.10-3.50)
115 = Lo (1 + 150.10-3)
115 = Lo (1 + 0.15)
115 = Lo (1.15)
Lo = 115 / 1.15
Lo = 100 cm
3. The initial length of a brass rod is 40 cm. After heated, the final length of the brass is 40.04 cm and the final temperature is 80oC. If the coefficient of linear expansion of the brass is 2.0 x 10-5 oC–1, what is the initial temperature of the brass rod.
Known :
The final temperature (T2) = 80oC
The initial length (Lo) = 40 cm
The final length (L) = 40.04 cm
The increase in length (ΔL) = 40.04 cm – 40 cm = 0.04 cm
The coefficient of linear expansion (α) = 2.0 x 10-5 oC-1
Solution : Initial temperature (T1)
Solution ;
The equation of the linear expansion :
L = Lo + α Lo ΔT
L – Lo = α Lo ΔT
ΔL = α Lo ΔT
ΔL = α Lo (T2 – T1)
0.04 = (2.0 x 10-5)(40)(80 – T1)
0..04 = (80 x 10-5)(80 – T1)
0.04 = 0.0008 (80 – T1)
0.04 = 0.064 – 0.0008 T1
0..0008 T1 = 0.064 – 0.040
0.0008 T1 = 0.024
T1 = 30oC
4. Two metal rods with the same size but different type, as shown in figure below. The thermal conductivity of metal I = 4 times the thermal conductivity of metal II. What is the temperature between both metals.
Known :
The size of both rods is the same.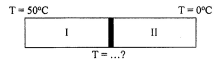
The thermal conductivity of metal I = 4k
The thermal conductivity of metal II = k
The temperature of the one end of metal I = 500 C
The temperature of the one end of metal II = 00 C
Wanted: The temperature between both the metal rods
Solution :
The equation of the heat conduction :
![]()
Q/t = the rate of heat conduction, k = thermal conductivity, A = the cross-sectional area, T1-T2 = the change in temperature, l = the length of the rod.
The temperature between both rods :
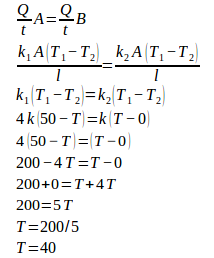
The temperature at the center between both the metals rods is 40oC.
5.
(1) Conductivity of metal
(2) The difference of temperature
(3) The length of metal
(4) Mass of metal
Factors that determine the rate of heat conduction on metals are…..
Solution :
Based on the equation of heat conduction, factors that determine the rate of heat conduction on metals are conductivity of metal (k), the difference of temperature (T) and the length of metal (l).
6. Two rods of the same size but different type, as shown in the figure below. The thermal conductivity of rod P is 2 times the thermal conductivity of rod Q. What is the temperature between both rods.
Known :
Both rods have the same size.![]()
Thermal conductivity of rod P (kP) = 2k
The thermal conductivity of rod Q (kQ) = k
Wanted: The temperature between both rods
Solution :
The equation of the heat conduction :
![]()
Q/t = the rate of heat conduction, k = thermal conductivity, A = the cross-sectional area, T1-T2 = the change in temperature, l = the length of the rod.
The temperature at the center between both rods :
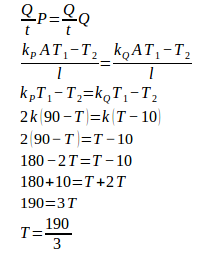
8. 100-gram oil at 20oC and 50-gram iron at 75 oC are placed in 200-gram iron container. The increase in temperature of the container is 5oC and the specific heat of oil is 0.43 cal/g oC. What is the specific heat of the iron?
Known :
Mass of iron container (m) = 200 gr
The initial temperature of the iron container (T1) = the temperature of oil = 20oC
The final temperature of the iron container (T2) = 20oC + 5oC = 25oC
Mass of oil (m) = 100 gram
The specific heat of oil (coil) = 0.43 cal/g oC
The initial temperature of oil (T1) = 20oC
The final temperature of oil (T2) = 20oC + 5oC = 25oC
Mass of iron (m) = 50 gram
The initial temperature of oil (T1) = 75oC
The final temperature of oil (T2) = 25oC
Wanted : The specific heat of iron (c iron)
Solution :
Heat released by iron :
Q = m c ΔT = (50)(c)(75-25) = (50)(c)(50) = 2500c calorie
Heat absorbed by the iron container :
Q = m c ΔT = (200)(c)(25-20) = (200)(c)(5) = 1000c calorie
Heat absorbed by oil :
Q = m c ΔT = (100)(0.43)(25-20) = (43)(5) = 215 calorie
Black principle states that in a isolated system, heat released by the hotter object, absorbed by the cooler object.
Q release = Q absorb
2500c = 1000c + 215
2500c – 1000c = 215
1500c = 215
c = 215/1500
c = 0.143 cal/g oC
9. A 200-gram water at 20°C placed in 50-gram ice at -2°C. If the change of heat just between water and ice, what is the final temperature of the mixture? The specific heat of water is 1 cal/gr°C, the specific heat of ice is 0.5 cal/gr°C, the heat of fusion for ice is 80 cal/gr.
Known :
Mass of water (mwater) = 200 gram
Temperature of water (Twater) = 20oC
The specific heat of water (cwater) = 1 cal/gr°C
Mass of ice (mice) = 50 gram
Temperature of ice (Tice) = -2oC
The specific heat of ice (cice) = 0.5 cal/gr°C
The heat of fusion for ice (L) = 80 cal/gr
Solution :
Heat to increases ice from -2oC to 0oC :
Q = m c ΔT
Q = (50 gram)(0.5 cal/gr°C)(0oC – (-2oC))
Q = (50)(0.5 cal)(2)
Q = 50 calorie
Heat for melting all ice :
Q = m L = (50 gram)(80 cal/gram) = 4000 calorie
Heat for decrease temperature of all water from 20oC to 0oC :
Q = m c ΔT
Q = (200 gram)(1 cal/gr°C)(0oC – (20oC))
Q = (200)(1 cal)(-20)
Q = -4000 calorie
Plus sign indicates that the heat is added, the minus sign indicates that heat released.
50-calorie of heat needed to increase the temperature of ice to 0oC and 4000-calorie needed to melting all ice. Total heat = 4050 calorie. The heat released by water is 4000 calorie.
Some of the ice not melting, so the final temperature of ice and water is 0oC.
10. A 200-gram aluminum at 20oC placed in 100-gram water at 80oC in a container. The specific heat of aluminum is 0.22 cal/g oC and the specific heat of water is 1 cal/g oC. What is the final temperature of aluminum?
Known :
Mass of aluminum = 200 gram
Temperature of aluminum = 20oC
Mass of water = 100 gram
Temperature of water = 80oC
The specific heat of aluminum = 0.22 cal/g oC
The specific heat of water = 1 cal/g oC
Wanted: The final temperature of aluminum
Solution :
Aluminum and water in thermal equilibrium so that the final temperature of aluminum = the final temperature of water.
Heat released by hot water (Q release) = heat absorbed by aluminum (Q absorb)
mwater c (ΔT) = maluminum c (ΔT)
(100)(1)(80 – T) = (200)(0.22)(T – 20)
(100)(80 – T) = (44)(T – 20)
8000 – 100T = 44T – 880
8000 + 880 = 44T + 100T
8880 = 144T
T = 62oC
11. A 50-gram metal at 85 °C placed in 50 gram water at 29.8 °C. The specific heat of water = 1 cal.g —1 .°C—1. The final temperature is 37 °C. What is the specific heat of metal.
Known :
Mass of metal (mmetal) = 50 gram
Temperature of metal = 85oC
Mass of water (mwater) = 50 gram
Temperature of water = 29,8oC
The specific heat of water (cwater) = 1 cal.g -1 .°C-1
The final temperature of water = 37oC
Wanted : The specific heat of metal (c metal)
Solution :
Heat released by hot metal (Q release) = heat absorbed by water (Q absorb)
mmetal c (ΔT) = mwater c (ΔT)
(50)(c)(85 – 37) = (50)(1)(37 – 29.8)
(c)(85 – 37) = (1)(37 – 29.8)
48 c = 7.2
c = 0.15 cal.g -1 .°C-1
12. A block of ice with mass of 50-gram at 0°C and 200-gram water at 30°C, placed in a container. . If the specific heat of water is 1 cal.g– 1 °C –1 and the heat of fusion for ice is 80 cal.g –1. What is the final temperature of the mixture.
Known :
Mass of ice (mice) = 50 gram
The temperature of ice = 0°C
Mass of water (mwater) = 200 gram
Temperature of water = 30oC
The specific heat of water (cwater) = 1 cal.g– 1 °C –1
The heat of fusion for ice (Lice) = 80 cal.g –1
Wanted: The final temperature
Solution :
Estimate the final condition :
Heat released by water to decrease its temperature from 30oC to 0oC :
Qrelease = mwater cwater (ΔT) = (200)(1)(30-0) = (200)(30) = 6000
Heat needed to melting all ice :
Q = mice Lice= (50)(80) = 4000
Heat used to melting all ice is 4000, while heat released by water is 6000. Can be concluded that the final temperature of the mixture above 0oC.
Black principle :
Heat released by water = heat for melting all ice + heat to increase the temperature of ice.
(mwater)(cwater)(ΔT) = (mice)(Lice) + (mice)(cwater)(ΔT)
(200)(1)(30-T) = (50)(80) + (50)(1)(T-0)
(200)(30-T) = (50)(80) + (50)(T-0)
6000 – 200T = 4000 + 50T – 0
6000 – 4000 = 50T + 200T
2000 = 250T
T = 2000/250
T = 8oC
