Speed of transverse wave – problems and solutions
1.
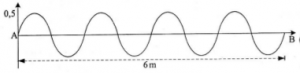
If the time interval required to travel from A to B is 2 seconds, determine the speed of the transverse wave.
Known :
Distance A-B = 6 meters
Time interval A-B = 2 seconds
Wanted: Speed of transverse wave
Solution :
1 wavelength has 1 crest and 1 trough. There is 4 wavelength between A and B. Distance between A and B is 6 meters so that 1 wavelength (λ) = 6 meters / 4 = 1.5 meters.
The time interval required to travel from A to B is 2 seconds so that the time interval required to travel 1 wavelength = period (T) = 2 seconds / 4 = 0.5 seconds.
The equation of the speed of wave :
v = λ f = λ / T
v = speed of wave, λ = wavelength, f = frequency, T = period
The speed of wave :
v = 1.5 meters / 0.5 seconds
v = 3 meters/second
2. If the time interval required to travel from A to B is 8 seconds, determine the speed of transverse wave.
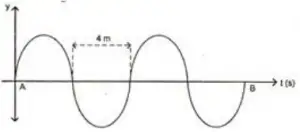
Known :
There are two wavelength.
1 wavelength (λ) = 2 x 4 meters = 8 meters
Period (T) = 8 seconds / 2 wavelengths = 4 seconds / wavelength
Wanted : Speed of wave (v)
Solution :
The speed of wave calculated using the equation of the speed of wave :
v = f λ = λ/T
v = 8 meters / 4 seconds
v = 2 meters/second
