Energy in a monatomic ideal gas
The energy in the monatomic ideal gas is the total amount of translational kinetic energy of monatomic ideal gas molecules. The total amount of translational kinetic energy of the ideal gas molecules = the product of the average translational kinetic energy of each molecule and the number of molecules (N). Mathematically:
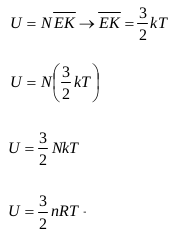
U = Energy in a monatomic ideal gas (J)
N = Number of molecules
k = Boltzmann constant (k = 1.38 x 10-23 J / K)
T = absolute temperature (K)
n = Number of moles (mol)
R = universal gas constant (R = 8.315 J / mol. K = 8315 kJ / kmol. K)
Energy in a diatomic ideal gas
Energy in an ideal diatomic gas is the total amount of translational kinetic energy, rotational kinetic energy and vibrational kinetic energy of the diatomic ideal gas molecules. By the principle of energy equipartition, the energy in an ideal diatomic gas is:
![]()
Energy in an ideal polyatomic gas
Energy in an ideal polyatomic gas is the total amount of translational kinetic energy, rotational kinetic energy and vibration kinetic energy of polyatomic ideal gas molecules. By the principle of energy equipartition, the energy in an ideal polyatomic gas is:
![]()
Energy in real gas
Energy in real gas also depends on temperature. When real gas pressure is large enough (small real gas volume), real gas starts to show deviant behavior. Therefore, it can be said that energy in a real gas also depends on pressure and volume.
