Electrostatic force – problems and solutions

Electrostatic force – problems and solutions

1. If the static electric force is 144 N, what is the distance between both charges… (1 μC = 10^-6 C and k = 9.10⁹ N.m².C^-2)

Known :

Electric force (F₁₂) = 144 N

Charge 1 (q₁) = 10 μC = 10 x 10^-6 C

Charge 2 (q₂) = 4 μC = 4 x 10^-6 C

Constant (k) = 9 x 10⁹ N.m².C^-2

C = Coulomb, N = Newton, m = meter

Wanted : Distance between both charges (r)

Solution :

The equation of Coulomb’s law :

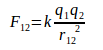
F = the static electric force, k = Coulomb’s constant, q = electric charge, r = distance between both charges

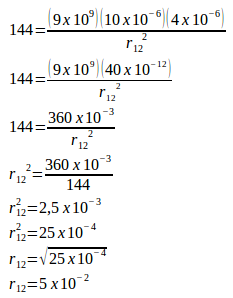
Distance between both charges (r) = 5 x 10^-2 meter = 5 x 10^-2 x 10² cm = 5 cm.

2. Two charges separated by a distance of r. If the static electric force is 3.6 N, what is the distance between both charges (1 μC = 10^-6 C and k = 9.10⁹ N.m².C^-2)

Known :

Electric force (F₁₂) = 3.6 N

Charge 1 (q₁) = 9 μC = 9 x 10^-6 C

Charge 2 (q₂) = 4 μC = 4 x 10^-6 C

Coulomb’s constant (k) = 9 x 10⁹ N.m².C^-2

C = Coulomb, N = Newton, m = meter

Wanted : Distance between both charges (r)

Solution :

Distance between both charges (r) = 0.3 m = 0.3 x 100 cm = 30 cm.

3. Three point charges as shown in figure below. What is the magnitude of the static electric force at point A (k = 9.10⁹ N.m².C^-2; 1 μ = 10^-6)

Known :

Charge A (q_A) = -2 μC = -2 x 10^-6 C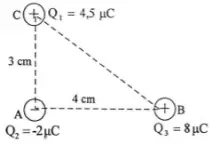

Charge B (q_B) = 8 μC = 8 x 10^-6 C

Charge C (q_C) = 4,5 μC = 4,5 x 10^-6 C

Coulomb‘s constant (k) = 9 x 10⁹ N.m².C^-2

Distance between charge A and B (r_AB) = 4 cm = 4 x 10^-2 m

Distance between charge A and C (r_AC) = 3 cm = 3 x 10^-2 m

C = Coulomb, N = Newton, m = meter

Wanted : The static electric force at point A

Solution :

The equation of Coulomb’s law :

F = the static electric force, k = Coulomb‘s constant, q = electric charge, r = distance between both charges

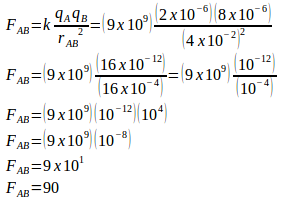
The static electric force at point A :

4. Three-point charges as shown in the figure below. What is the magnitude of Coulomb force experienced by Charge B (k = 9.10⁹ N.m².C^-2; 1 μC = 10^-6 C).

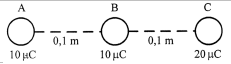
Known :

q_A = 10 µC = 10 x 10^-6 C = 10^-5 Coulomb

q_B = 10 µC = 10 x 10^-6 = 10^-5 Coulomb

q_C = 20 µC = 20 x 10^-6 = 2 x 10^-5 Coulomb

r_AB = 0.1 meter = 10^-1 m

r_BC = 0.1 meter = 10^-1 m

k = 9 x 10⁹ Nm²C⁻²

Wanted : Coulomb force experienced by Charge B

Solution :

There are two coulomb forces act on charge B, Coulomb force between charge A and B (F_AB) and Coulomb force between charge B and C (F_BC). Coulomb force experienced by charge B is net force of F_AB and F_BC.

Coulomb force between charge A and B :

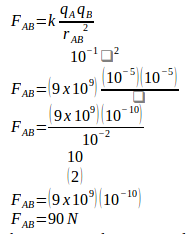
Charge A signed positive and charge B signed positive so that F_AB points to charge C.

Coulomb force between charge B and C :

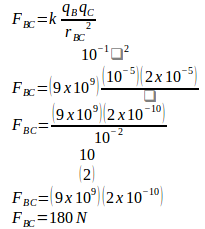
Charge B signed positive and charge C signed positive so that F_BC points to charge A.

Coulomb force experienced by charge B :

F_B = F_BC – F_AB = 180 – 90 = 90 N

Coulomb force experienced by charge B (F_B) is 90 Newton. The direction of F_B same as the direction of F_BC points to charge A.

5. Determine the magnitude and direction of Coulomb force on charge B (k = 9 x 10⁹ Nm²C⁻², 1 μC = 10⁻⁶ C).

Known :

Charge A (q_A) = +Q

Charge B (q_B) = -2Q

Charge C (q_C) = -Q

Distance between charge A and B (r_AB) = r

Distance between charge B and C (r_BC) = 2r

k = 9 x 10⁹ Nm²C⁻²

Wanted : Magnitude and direction of Coulomb force on charge B

Solution :

Coulomb force between charge A and B :

Charge A positive and charge B negative so that the direction of F_AB points to charge A.

Coulomb force between charge B and charge C :

Charge B is negative and charge C is negative so that the direction of F_BC points to charge A.

Net force act on charge B :

F = F_AB + F_BC = 2 k Q²/r² + 0.5 k Q²/r² = 2.5 k Q²/r² = 2.5 k Q² r^-2

Direction of force points to charge A or to leftward.