Addition of Vectors

Article about the Addition of Vectors

1. Quantities of vector and scalar

In addition to the fundamental and derived quantities, physical quantities can still be divided into two other types, namely scalar quantities and vector quantities. Quantities such as mass, distance, time and volume, are scalar quantities, quantities that only have magnitude but have no direction. Whereas magnitudes such as displacement, velocity, acceleration, and force are vector quantities, quantities that have magnitude and also have direction.

a. Difference between scalar and vector quantity

If you say the mass of a ball is 400 grams, this statement is enough for you to know the mass of the ball. You don’t need direction to find out the mass of the ball. Likewise with time, temperature, volume, density, etc. There are several physical quantities that cannot be expressed in magnitude only. If you say a child moves as far as 100 meters, then this statement is not enough. You might ask, where did he move? Is it north, south, east, or west? Likewise, if you say that you push the table with a force of 200 N.

Where do you drive? Well, such quantities are called vector quantities, which require an explanation of the magnitude and direction. Examples of vector quantities are displacement, acceleration, impulse, momentum, etc. You can understand it more clearly when studying subjects related to that quantities.

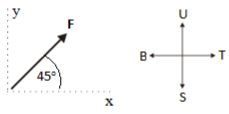b. Draw a vector

Vector is indicated by an arrow. The arrow is always drawn so that it points in the direction of the vector. The length of the arrow is described as the magnitude of the vector. For example, in the figure of a vector of force (F) with a magnitude of 2 N whose direction is towards the northeast or 45^o about the x-axis.

c. Rules for writing quantities of vector

In writing a vector, if you use handwriting, the symbol of a vector is generally written in italics using uppercase letters, and above it needs to be added with an arrow. For printed books, vector symbols are written in uppercase letters in bold, for example, F. For the magnitude of the vector, if we use handwriting then the magnitude of a vector is written, for example, |F|. For printed books, the magnitude of a vector is written in italics, for example, F.

2. Addition of vectors—graphical methods

There are several ways to add vectors graphically, including the Tail-to-tip method and the parallelogram method.

a. Tail-to-tip method of adding vectors

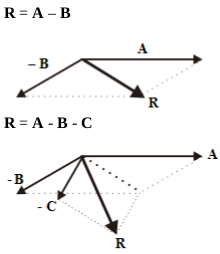
Vector A and B are known. Vector A = 3 cm coincides with the x-axis (towards the east). Vector B = 2 cm forms an angle of 30^o to the x-axis (towards the northeast). Add A and B graphically using the Tail-to-tip method. a) R = A + B b) R = A – B

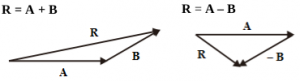
The magnitude of the resultant vector (R) is measured using a ruler. The direction of the resultant vector is measured using a protractor.

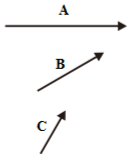
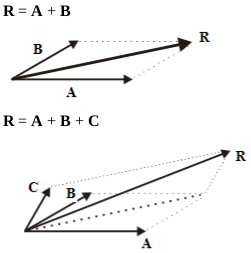
Known vectors A, B, and C. Vector A = 3 cm coincides with the x-axis (towards the east). Vector B = 2 cm forms an angle of 30^o to the x-axis (towards the northeast). Vector C = 1 cm forms an angle of 60^o to the x-axis (towards the northeast). Add A, B, and C graphically using the Tail-to-tip method.

a) R = A + B + C

b) R = A – B – C

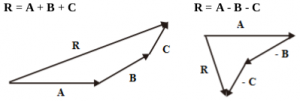
The resultant vector (R) is measured using a ruler. The direction of the resultant vector is measured using a protractor.

b. Parallelogram method

Known vectors A, B, and C. Vector A = 3 cm coincides with the x-axis (towards the east). Vector B = 2 cm forms an angle of 30^o to the x-axis (towards the northeast). Vector C = 1 cm forms an angle of 60^o to the x-axis (towards the northeast). Add A, B, and C graphically using a parallelogram.

a) R = A + B

b) R = A – B

c) R = A + B + C

d) R = A – B – C

The resultant vector (R) is measured using a ruler. The direction of the resultant vector is measured using a protractor.

3. Addition of vectors – analytical method

Determining the magnitude and direction of the resultant vector with the graphical method is one approach. The accuracy of the results depends on your accuracy and accuracy in drawing and reading the scale. The magnitude and direction of the resultant vector are more precisely obtained through mathematical calculations.

a. Calculating the sum of 2 vectors using the cosine rule

The formula for determining the magnitude of the resultant vector:

The formula for determining the direction of the resultant vector:

C = resultant vector

A = vector 1

B = vector 2

cos ∠(A, B) = angle formed by vectors A and B

Sample problem 1:

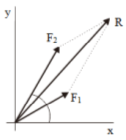
F₁ = 2 N forms an angle of 30 about x-axis, F₂ = 3 N forms an angle of 60^o about x-axis, θ = 30^o.

Sample problem 2:

F₁ = 2 N coincides with the x-axis, F₂ = 3 N forms an angle of 90^o about x-axis, θ = 90^o.

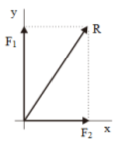
b. Adding vectors by components

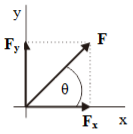
Review a vector F that forms a certain angle about the x-axis, as shown in the figure below. F_x and F_y are component vectors of vector F.

The magnitude of the component vector is determined using the formula:

F_x = F cos θ

F_y = F sin θ

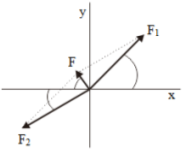
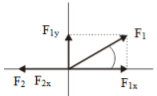
Review the two vectors F₁ and F₂ which form a certain angle about the x-axis, as shown in the figure below. F_1x and F_1y are components of vector F₁, so F_2x and F_2y are components of vector F₂.

The component vector is determined using the formula:

F_1x = F₁ cos θ

F_1y = F₁ sin θ

F_2x = F₂ cos θ

F_1y = F₁ sin θ

Adding the component vectors:

F_x = F_1x + F_2x

F_y = F_1y + F_2y

The resultant vector is determined using the formula:

The direction of the resultant vector is determined using the formula:

Sample problem 1:

Determine the components of vector F whose magnitude is 20 N and form an angle of 30^o about the x-axis.

F_x = (20 N)(cos 30^o) = 17 N

F_y = (20 N)(sin 30^o) = 10 N

Sample problem 2:

F₁ = 20 N forms an angle of 30^o about the x-axis and F₂ = 15 N forms an angle of 180o about the x-axis. Determine the magnitude and direction of the resultant vector.

F_1x = (20 N)(cos 30^o) = 17 N

F_2x = F₁ = – 15 N

F_1y = (20 N)(sin 30^o) = 10 N

F_2y = 0

Adding the component vectors:

F_x = F_1x – F_2x = 17 N – 15 N = 2 N

F_y = 10 N

The resultant vector:

F₂ = F_x² + F_y² = 2² + 10² = 4 + 100 = 104

F = 10.2 N

Direction of the resultant vector:

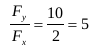
θ = tan−15 = 78.7^o about the x-axis

Sample problem 3 :

F₁, F_2, and F₃ are 20 N, 30 N and 40 N. F₁ forms an angle of 60^o about the x-axis, F₂ forms an angle of 150^o about the x-axis, and F₃ forms an angle of 315^o about the x-axis. Determine the magnitude and direction of the resultant vector.

F_1x = (20 N)(cos 60^o) = 10 N

F_1y = (20 N)(sin 60^o) = 17 N

F_2x = (30 N)(cos 30^o) = -26 N

F_2y = (30 N)(sin 30^o) = 15 N

F_3x = (40 N)(cos 45^o) = 28 N

F_3y = (40 N)(sin 45^o) = -28 N

Adding the component vector:

F_x = F_1x – F_2x + F_3x = 10 N – 26 N + 28 N = 12 N

F_y = F_1y + F_2y – F_3y = 17 N + 15 N – 28 N = 4 N

Resultant vector:

F² = F_x² + F_y² = 12² + 4² = 144 + 16 = 160

F = 13 N

Direction of the resultant vector:

θ = tan⁻¹ 0.3 = 17^o about the x-axis