Solved Problems in Linear Motion – Freely falling objects
1. An object dropped from the top of a cliff. It is seen to hit the ground below after 3 seconds. Determine its velocity just before hitting the ground. Acceleration of gravity is 10 m/s2. Ignore air resistance.
Known :
Initial velocity (vo) = 0 (object dropped)
Time interval (t) = 3 seconds
Acceleration of gravity (g) = 10 m/s2
Wanted : Final velocity (vt)
Solution :
Acceleration due to gravity at the surface of the earth, its magnitude is 9.8 m/s2. To make calculation easier, we use 10 m/s2.
10 m/s2 or 10 m/s / 1 second, means that the speed increases linearly in time by 10 m/s during each second.
After 1 second, object’s speed = 10 m/s
After 2 seconds, object’s speed = 20 m/s
After 3 seconds, object’s speed = 30 m/s.
We also can use kinematic equations for motion at a constant acceleration, as shown below.
vt = vo + a t
s = vo t + ½ a t2
vt2 = vo2 + 2 a s
Free fall has no initial velocity (vo = 0), so above equation can be changed as shown below :
Equation of Free fall motion :
vt = g t ………… 1
h = ½ g t2 ………… 2
vt2 = 2 g h ………….. 3
vt = g t
vt = (10)(3)
vt = 30 m/s
Final velocity is 30 m/s
2. A body falls freely from rest, from a height of 25 m. Find (a) The speed with which it strikes the ground. (b) The time it takes to reach the ground.
Acceleration due to gravity at the surface of Earth is 10 m/s2.
Known :
Height (h) = 5 meters
Acceleration of gravity (g) = 10 m/s2
Wanted :
(a) Final velocity (vt)
(b) Time interval (t)
Solution :
Free fall’s equation :
vt = g t
h = ½ g t2
vt2 = 2 g h
(a) Final velocity (vt)
vt2 = 2 g h = 2(10)(5) = 100
vt = 10 m/s
(b) Time interval (t)
h = ½ g t2
5 = ½ (10) t2
5 = 5 t2
t2 = 5/5 = 1
t = 1 second
3. A ball dropped from a height. Find (a) Acceleration (b) Distance after 3 seconds (c) Time in air if final velocity is 20 m/s. Acceleration due to gravity = 10 m/s2
Known :
Acceleration of gravity (g) = 10 m/s2
Wanted :
(a) Acceleration (a)
(b) Distance or height (h) if time elapsed (t) = 3 seconds
(c) Time interval (t) if vt = 20 m/s
Solution :
Free fall’s equation :
vt = g t
h = ½ g t2
vt2 = 2 g h
(a) Acceleration (a)
Acceleration = acceleration due to gravity = 10 m/s2. It means speed increase by 10 m/s each second.
(b) Distance or height (h) after t = 3 seconds
h = ½ g t2 = ½ (10)(3)2 = (5)(9) = 45 meters
(c) Time elapsed (t) if vt = 20 m/s
vt = g t
20 = (10) t
t = 20 / 10 = 2 seconds
[wpdm_package id=’511′]
[wpdm_package id=’517′]
- Distance and displacement
- Average speed and average velocity
- Constant velocity
- Constant acceleration
- Free fall motion
- Down motion in free fall
- Up and down motion in free fall


 Car A moving with a constant speed at 10 meters/second, means car A moves as far as 10 meters every 1 second. After 2 seconds, A car move as far as 20 meters.
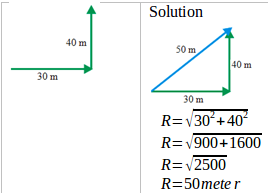
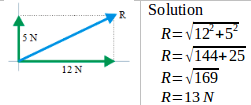
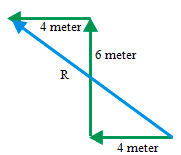
Car A moving with a constant speed at 10 meters/second, means car A moves as far as 10 meters every 1 second. After 2 seconds, A car move as far as 20 meters.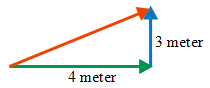 Distance = 4 meters + 3 meters = 7 meters
Distance = 4 meters + 3 meters = 7 meters Solution
Solution
 F
F

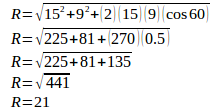

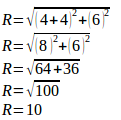
 Solution
Solution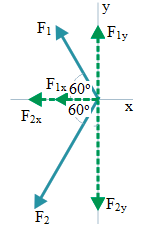 Solution
Solution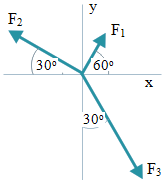 Solution
Solution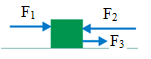 Solution
Solution